統計検定2級CBT公式問題集の解説(2変数記述統計の分野)
2023/07/12
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問1:散布図と度数分布に関する問題
- 問2:散布図の読み取りに関する問題
- 問3:散布図の選択に関する問題
- 問4:散布図と相関・範囲に関する問題
- 問5:相関係数からの共分散計算に関する問題
- 問6:相関関係の記述に関する問題
問1
ヒストグラムは「女性の50歳時未婚率」なので、散布図の縦軸に注目します。
散布図の中で女性の50歳時未婚率8%〜10%に該当するデータは2個、もしくは3個(うち1つのデータは10%ちょうどくらいなので、8%〜10%のカテゴリーに入るか入らないか微妙です)あります。この条件を満たすのは、①③のみです。
次に、散布図の中で女性の50歳時未婚率10%〜12%に該当するデータは12個、もしくは13個(はっきりした数はわかりませんが少なくとも10個以上)あります。この条件を満たすのは、①③のうち③のみです。
このように、散布図から該当するヒストグラムを探す場合には、
- 最小、もしくは最大の階級
- ヒストグラム間で大きく度数が異なっている階級
におけるデータの個数に着目すると、比較的簡単にヒストグラムを絞り込むことができます。
散布図の詳細については「26-1. 散布図」をご覧ください。
問2
1:× 1990年における女性の50歳時未婚率なので左側の散布図の縦軸に注目すると、8%を超えている点は1つしかないことが分かります。
2:× 1990年における男性の50歳時未婚率なので左側の散布図の横軸に注目すると、10%を超えている点が2つあることが分かります。
3:× 1990年における男性の50歳時未婚率は大体2%〜11%の範囲に収まっています。一方、2015年における男性の50歳時未婚率は大体18%〜27%の範囲に収まっています。つまり、すべての都道府県において2015年の男性の50歳時未婚率は1990年の男性の50歳時未婚率を上回っていると言えます。
4:○ 2015年における女性の50歳時未婚率は大体8%〜20%の範囲に収まっています。一方、2015年における男性の50歳時未婚率は大体18%〜27%の範囲に収まっています。散布図をよく見ると、女性の50歳時未婚率が18%を超えている都道府県は1つのみであり、それ以外の都道府県はすべて2015年の男性の50歳時未婚率が2015年の女性の50歳時未婚率を上回っています。 女性の50歳時未婚率が18%を超えている都道府県のみ個別に見てみると、男性の50歳時未婚率は約26%であることから、2015年の男性の50歳時未婚率が2015年の女性の50歳時未婚率を上回っています。したがって、すべての都道府県において2015年の男性の50歳時未婚率は1990年の女性の50歳時未婚率を上回っていると言えます。
5:× 2015年において女性の50歳時未婚率が最も低い都道府県は、男性の50歳時未婚率が約19%になっています。この値よりも男性の50歳時未婚率が低い都道府県があることから、女性の50歳時未婚率が最も低い都道府県は男性の50歳時未婚率も最も低いとは言えません。
問3
国語と英語のそれぞれの分散、および共分散の値が与えられているので、相関係数を計算することができます。2つの要素 ![]() と
と ![]() からなる
からなる ![]() 個のデータ(
個のデータ(![]() ,
, ![]() :
: ![]() )が得られたとき、その相関係数
)が得られたとき、その相関係数![]() は次の式から算出されます。
は次の式から算出されます。
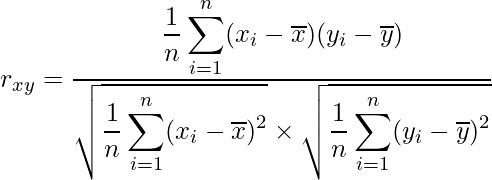
分子の
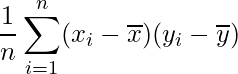
は「共分散」とよばれるものです。共分散は2つの変数の関係を表すもので、一方の変数の値が増加するときにもう一方の変数の値も増加する場合には、共分散は正の値を取ります。逆に、一方の変数の値が増加(減少)するときにもう一方の変数の値は減少(増加)する場合には、共分散は負の値を取ります。ただし、共分散はデータの値をそのまま用いて計算するため、データの単位の影響を受けてしまい、共分散の値の大小を単純に比較することができません。
そこで、共分散を2つの変数それぞれにおける標準偏差で割って正規化します。この値が「相関係数」です。相関係数は必ず−1から1までの値をとるため、様々なデータから計算された相関係数どうしを比較することができます。
与えられた分散と共分散の値を式に入れると、相関係数 ![]() は
は
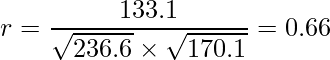
となります。この結果から、やや強い正の相関が見られた散布図を探します。正の相関が見られる散布図は①③④です(②は正の相関か負の相関化か分からないくらい弱い相関、⑤は強い負の相関)。①は強い正の相関、④は弱い正の相関であることから、①が条件を満たす散布図であることが分かります。
相関係数の詳細については「26-3. 相関係数」をご覧ください。
問4
I:○ 中央の散布図を見ると、日平均気温と日最高気温の間に正の相関があることが分かります。
II:○ 右側の散布図の横軸を見ると、日最低気温の点は−2℃から12℃(範囲は14℃)の間に収まっています。同様に、右側の散布図の縦軸を見ると、日最高気温の点は5℃から25℃(範囲は20℃)の間に収まっています。すなわち、日最低気温のほうが日最高気温より範囲が小さいことが分かります。
III:× 左側の散布図を見ると、日平均気温と日最低気温の間には正の相関があることが分かります。
問5
問3とは逆パターンで、相関係数から共分散を求める問題です。2つの要素 ![]() と
と ![]() からなる
からなる ![]() 個のデータ(
個のデータ(![]() ,
, ![]() :
: ![]() )が得られたとき、その相関係数
)が得られたとき、その相関係数![]() は次の式から算出されます。
は次の式から算出されます。
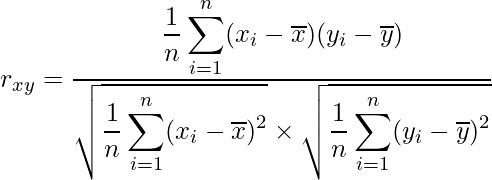
分子の
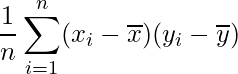
が共分散であることから、この値を ![]() とおきます。与えられた標準偏差と相関係数の値を式に入れると、
とおきます。与えられた標準偏差と相関係数の値を式に入れると、
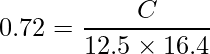
となります。これを解くと、共分散の値を得ることができます。
問6
「国語100点、英語20点」の点と、「国語20点、英語100点」の点を結んだときに、その直線よりも上にある点が合格者の集団です。
受験者全体では両方の科目の点数が高い右上の方から、両方の科目の点数が低い左下の方までだらだらと伸びた分布しています。一方、合格者の集団はだらだらと伸びた分布を真ん中辺りからぶった切ったような分布になります。すなわち、受験者全体の分布と比べて直線的な関係が弱くなる=相違関係数が小さくなります。








