令和元年 公認会計士試験論文式試験(統計学)第8問 問題2
2021/06/25
カテゴリ:公認会計士(統計学)
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
問1
- 仮説を立てる
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説は「卵のパックの重さは750gである」とします。したがって、対立仮説は「卵のパックの重さは750gではない」とします。
この実験では母分散が分かっているので、母分散を用いる統計量Zを使います。統計量Zは次の式から求められます。![]() はデータの標本平均、
はデータの標本平均、![]() は母平均、
は母平均、![]() は母分散、
は母分散、![]() はサンプルサイズを表します。
はサンプルサイズを表します。
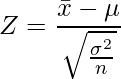
検定統計量Zは正規分布に従うことから、この検定で使用する分布は「正規分布」です。また、この卵パックの重さが750gであるかどうか(母平均が750gであるかどうか)を調べることが目的なので、両側検定を行います。統計数値表から![]() の値を読み取ると「1.96」となっています。つまり、棄却域は
の値を読み取ると「1.96」となっています。つまり、棄却域は![]() となります。
となります。
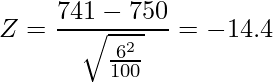
![]() は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり、「この卵パックの重さは750gではなく、表示は妥当ではない」と結論づけられます。
は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり、「この卵パックの重さは750gではなく、表示は妥当ではない」と結論づけられます。
問2
- 仮説を立てる
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説は「卵のパックの重さは1週間前と同じ741gである」とします。したがって、対立仮説は「卵のパックの重さは1週間前より減少した」とします。
この実験では母分散が分かっているので、母分散を用いる統計量Zを使います。この問題では平均値の差の検定を行う必要があります。この場合の統計量Zは次の式から求められます。![]() はデータ1の標本平均、
はデータ1の標本平均、![]() はデータ2の標本平均、
はデータ2の標本平均、![]() は母分散、
は母分散、![]() はデータ1のサンプルサイズ、
はデータ1のサンプルサイズ、![]() はデータ2のサンプルサイズを表します。
はデータ2のサンプルサイズを表します。
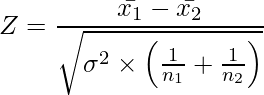
検定統計量Zは正規分布に従うことから、この検定で使用する分布は「正規分布」です。また、この卵パックの平均重量が1週間前に比べて減少したを調べることが目的なので、片側検定を行います。統計数値表から![]() の値を読み取ると「1.645」となっています。つまり、棄却域は
の値を読み取ると「1.645」となっています。つまり、棄却域は![]() となります。
となります。
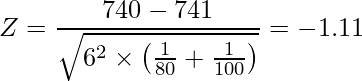
![]() は棄却域に入っていないことから、「有意水準5%において、帰無仮説を棄却しない」という結果になります。つまり、「卵のパックの重さは1週間前より減少したとは言えない」と結論づけられます。
は棄却域に入っていないことから、「有意水準5%において、帰無仮説を棄却しない」という結果になります。つまり、「卵のパックの重さは1週間前より減少したとは言えない」と結論づけられます。
問3
- 仮説を立てる
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説は「卵のパックの重さは750gである」とします。したがって、対立仮説は「卵のパックの重さは750gではない」とします。
この実験では母分散ではなく不偏分散が分かっているので、不偏分散を用いる統計量tを使います。統計量tは次の式から求められます。![]() はデータの標本平均、
はデータの標本平均、![]() は母平均、
は母平均、![]() は不偏分散、
は不偏分散、![]() はサンプルサイズを表します。
はサンプルサイズを表します。
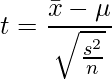
検定統計量tはt分布に従うことから、この検定で使用する分布は自由度「10-1=9」の「t分布」です。また、この卵パックの重さが750gであるかどうか(母平均が750gであるかどうか)を調べることが目的なので、両側検定を行います。統計数値表から![]() の値を読み取ると「2.262」となっています。つまり、棄却域は
の値を読み取ると「2.262」となっています。つまり、棄却域は![]() となります。
となります。
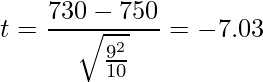
![]() は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり、「この卵パックの重さは750gではなく、表示は妥当ではない」と結論づけられます。
は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり、「この卵パックの重さは750gではなく、表示は妥当ではない」と結論づけられます。








