※コラム「統計備忘録」の記事一覧はこちら※

2人の鑑定家 A と B が、ゴッホの作品と思われている 100枚の絵画を鑑定しました。Aは 40枚が真作で 60枚が贋作、Bは真作も贋作も半々の 50枚ずつであるとの鑑定を下しました。2人の鑑定が一致したのは真作が 30枚と贋作が 40枚で合わせて 70枚です。

このような場合、2人の鑑定が、どの程度一致していると考えればよいのでしょうか。一致の度合いを 0 から 1 の数値で表すことはできないでしょうか。一致度を計算してみたいと思います。

まず、何を 0 とするかです。2人の鑑定結果がまったく異なる根拠によるものであるなら、2人の鑑定結果が一致するのは偶然によってのみということも考えられます。偶然に鑑定が一致する絵の枚数の期待値は、次の表のように 2人が同じ判断になる確率を求め、さらに全体の絵の枚数を掛ければ推測できます。

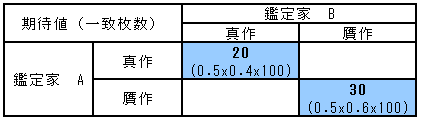
一致度が 0 でも（偶然だけでも）、 真作 20枚と贋作 30枚 の合わせて 50枚は、鑑定が一致する可能性が高いだろうと言えます。この計算は、「独立性の検定」の記事で紹介した「独立性の検定で完全に帰無仮説の期待度数を求める方法」と同じですが、利用するのはクロス集計表の対角要素、色のついたところだけです。

続いて、何を 1 とするかは、当然、100枚すべての真贋が一致したときということになります。この 100枚と 50枚の差である 50枚を一致度を計算するときの分母にします。

さて、2人の鑑定が一致した絵の枚数は 70枚でしたから、ここからも偶然だけで一致する場合の期待値 50枚を引きます。残りの 20枚が偶然以外で鑑定が一致した絵の枚数ということになります。最後に、この 20枚を先ほどの分母の50枚で割ってやります。20 / 50 = 0.4 が 2人の鑑定の一致度と言えそうです。この一致度のことをカッパ係数（Cohen's kappa coefficient）と呼びます。