線形混合モデル : Linear Mixed Model
概要
重回帰分析では、サンプルの独立性が仮定されますが、2段抽出法などで得られたデータはグループ内で相関が存在するなど、独立性を満たさない場合があります。このような場合、変量効果をもつ線形混合モデルを利用することで、グループ内の誤差構造を含めたモデリングが可能になります。
本製品では、Raudenbushの定義によるレベル2のモデルが分析可能です。推定方法は最尤法で、グループ間の共分散構造は無構造のみが指定可能です。
分析例ファイルのダウンロード
線形混合モデルを使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
データベース形式
| データサイズ範囲 | 処理対象データ | |||||
|---|---|---|---|---|---|---|
| 行数 | 列数 | カテゴリー数 | 数値 | 文字列 | 空白 | |
| 目的変数 | 3~60,000行 | 1列 | - | ○※1 | 欠 | 欠 |
| 説明変数(固定効果) | 3~60,000行 | 1~100列 | - | ○ | 欠 | 欠 |
| 説明変数(変量効果)※2 | 3~60,000行 | 1~15列 | - | ○ | 欠 | 欠 |
| 層 | 3~60,000行 | 1列 | 2~2000カテゴリー | ○ | 〇 | 〇 |
※:○…処理可、×…処理不可、欠…欠損値として除く
※2:変量効果は、固定効果に含めた説明変数から指定できます。
設定項目
Excelの[エクセル統計]タブから、[多変量解析]→[線形混合モデル]を選択すると以下のダイアログが表示されます。
「変数」タブ
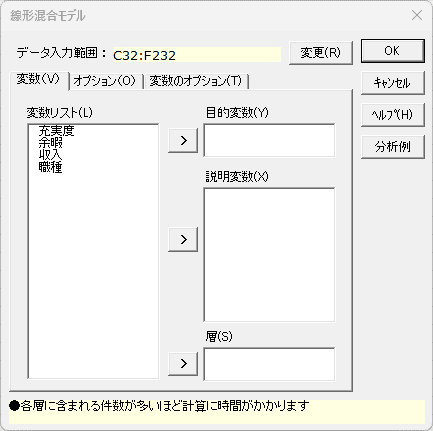
- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力範囲のダイアログが表示されるので、データ入力範囲を設定して [戻る] ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- 目的変数 必須
- [変数リスト]から目的変数とする変数を設定します。
- 説明変数
- [変数リスト] から説明変数とする変数を設定します。
- 層 必須
- [変数リスト] から層とする変数を設定します。
目的変数または説明変数に「空白」や「文字」が、層に「空白」が入力されているケースは分析対象から除かれ、目的変数と説明変数と層が全て揃っているケースが分析対象となります。
「オプション」タブ
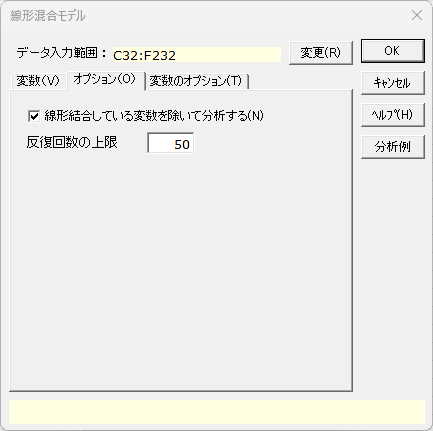
- 線形結合している変数を除いて分析する
- 線形結合している変数を最初に除いてから分析する場合、このチェックボックスをオンにします。初期設定はオンです。
- 反復回数の上限
- 線形混合モデルは最尤法により推定しています。推定の反復回数の上限を指定します。初期設定は50回です。
「変数のオプション」タブ
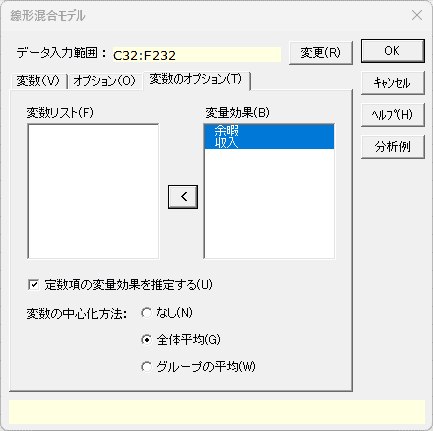
- 変量効果
- [変数リスト] から変量効果をモデルに含める変数を設定します。
- 定数項の変量効果を推定する
- 定数項の変量効果をモデルに含め分析する場合、このチェックボックスをオンにします。初期設定はオンです。
- 変数の中心化方法 必須
- 説明変数の中心化について、[変数リスト]、[全体平均]、[グループの平均] から選択します。
出力内容
| ケースの要約 | 有効ケース、目的変数のみ不明、説明変数のみ不明、ともに不明、全体の「サンプルサイズ」と「割合」 |
|---|---|
| 目的変数の要約 | 層のカテゴリーごとの「サンプルサイズ」と「割合」 |
| 基本統計量 | 説明変数と目的変数の各変数の「サンプルサイズ」、「平均」、「不偏分散」、「標準偏差」、「最小値」、「最大値」 |
| 相関行列 | 目的変数と説明変数間の相関係数の行列 |
| 線形結合している変数 | 説明変数間で線形結合している変数のリスト |
| 分析設定 | 分析実行時に指定した変数の中心化方法 |
| 回帰式の有意性 | 説明変数がない場合とある場合の「-2対数尤度」、「AIC」、「BIC」、及び「尤度比検定」により回帰式全体について有意性を検定した結果 |
| 偏回帰係数(固定効果)の推定 | 回帰式に含まれる各固定効果の「偏回帰係数」、「標準誤差」、「偏回帰係数の95%信頼区間」、「偏回帰係数の有意性の検定」の結果 |
| 分散成分(変量効果の推定) | 回帰式に含まれる各変量効果の「標準偏差」、「分散成分」、「分散成分の有意性の検定」の結果 |
| 変量効果の共分散行列/相関行列 | レベル2成分間の共分散行列と相関行列 |
| 変量効果の共分散行列の標準誤差 | レベル2成分間の共分散行列の標準誤差 |
参考文献
- S.W.Raudenbush, A.S.Bryk, "Hierarchical Linear Models Applications and Data Analysis Methods second edition", Sage Publications, 2002.


