- Step1. 基礎編
- 28. 等分散性の検定とWelchのt検定
28-1. F分布
F分布は、自由度が![]() 、
、![]() のカイ二乗分布
のカイ二乗分布![]() 、
、![]() が互いに独立である場合に、次の式から算出されるFが従う確率分布のことです。このときFは自由度(
が互いに独立である場合に、次の式から算出されるFが従う確率分布のことです。このときFは自由度(![]() ,
, ![]() )のF分布に従います。F分布はt分布やカイ二乗分布と同様、自由度によって形が異なる分布ですが、t分布やカイ二乗分布と異なり2つの自由度から分布の形が決まります。
)のF分布に従います。F分布はt分布やカイ二乗分布と同様、自由度によって形が異なる分布ですが、t分布やカイ二乗分布と異なり2つの自由度から分布の形が決まります。
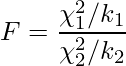
自由度が![]() と
と![]() のとき、F分布の確率密度関数は次の式で表すことができます(
のとき、F分布の確率密度関数は次の式で表すことができます(![]() )。
)。![]() はガンマ関数、
はガンマ関数、![]() はベータ関数を表します。F分布の式は非常に複雑ですが、覚える必要はありません。
はベータ関数を表します。F分布の式は非常に複雑ですが、覚える必要はありません。
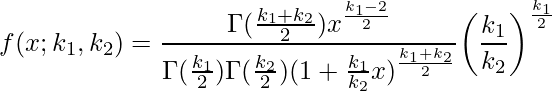
あるいは
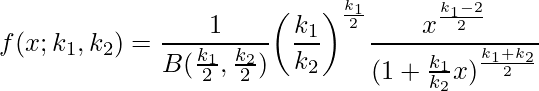
■F分布の実際の使い方
正規分布に従う2つの母集団が従う確率変数![]() 、
、![]() を考えます。これらの母集団からそれぞれサンプルサイズが
を考えます。これらの母集団からそれぞれサンプルサイズが![]() ,
, ![]() の標本を抽出したときの不偏分散をそれぞれ
の標本を抽出したときの不偏分散をそれぞれ![]() ,
, ![]() とします。このときFを求める式には次の関係が成り立ちます。また、Fは自由度(
とします。このときFを求める式には次の関係が成り立ちます。また、Fは自由度(![]() ,
, ![]() )のF分布に従います。
)のF分布に従います。
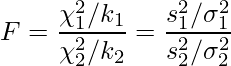
2つの母集団の母分散が等しいと仮定できるとき、上の式は
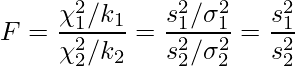
となることから、Fは帰無仮説![]() を「2標本の母分散は等しい(
を「2標本の母分散は等しい(![]() )」とした場合に、2標本の不偏分散を用いて母分散が等しいかどうかを検定する「等分散性の検定」に使われます。等分散性の検定については28-3章で説明します。
)」とした場合に、2標本の不偏分散を用いて母分散が等しいかどうかを検定する「等分散性の検定」に使われます。等分散性の検定については28-3章で説明します。
■F分布の形
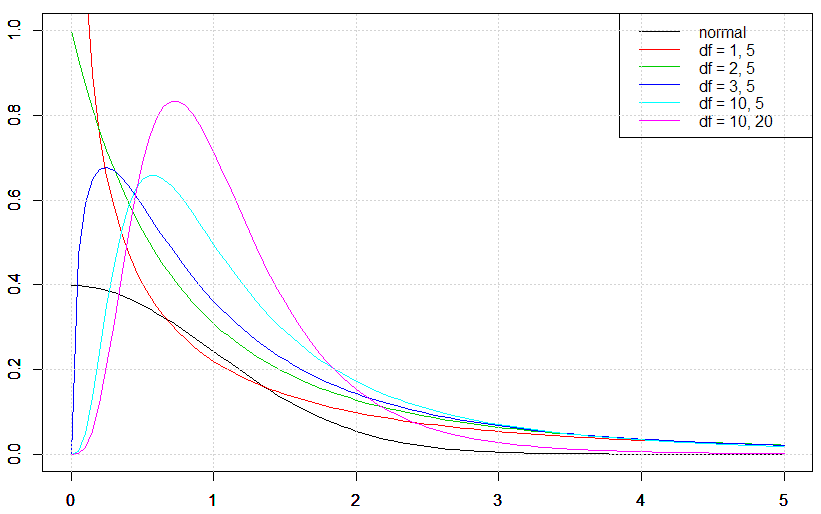
自由度を変化させた時のF分布の形を見てみます。次のグラフは自由度(![]() ,
, ![]() )(グラフ中ではdfで表示しています)が(1, 5)、(2, 5)、(3, 5)、(10, 5)、(10, 20)である場合のF分布(黒、赤、緑、青、水色、ピンク線)です。
)(グラフ中ではdfで表示しています)が(1, 5)、(2, 5)、(3, 5)、(10, 5)、(10, 20)である場合のF分布(黒、赤、緑、青、水色、ピンク線)です。
■F分布の性質
- 期待値と分散
確率変数
 が自由度(m, n)のF分布に従っている時、
が自由度(m, n)のF分布に従っている時、 の期待値
の期待値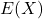 と分散
と分散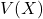 は次のようになります。
は次のようになります。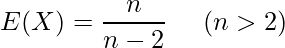
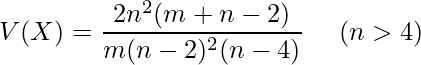
- t分布とF分布の関係
標準正規分布N(0, 1)に従うZと自由度nのカイ二乗分布Wがあり、これらが互いに独立であるとき、次の式から算出されるtは自由度nのt分布に従います(20-1章)。
上式の両辺を2乗すると、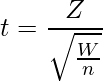 となりますが、自由度1のカイ二乗分布は標準正規分布に従う確率変数を2乗したものに等しくなるので(22-1章)、tが自由度のnのt分布に従うとき、
となりますが、自由度1のカイ二乗分布は標準正規分布に従う確率変数を2乗したものに等しくなるので(22-1章)、tが自由度のnのt分布に従うとき、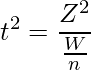
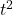 は自由度(1, n)のF分布に従います。
は自由度(1, n)のF分布に従います。
■おすすめ書籍
医学統計で使われる様々な手法をイラストによるイメージから理解することができます。イラストが凄く可愛らしいのと、世界観が面白いので個人的にお気に入りの1冊です。
28. 等分散性の検定とWelchのt検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 11. 確率変数と確率分布
11-4. 確率密度と確率密度関数
- 22. 母分散の区間推定
22-1. カイ二乗分布








