- Step1. 基礎編
- 25. さまざまな検定
25-7. 母比率の差の検定
25-1章では母比率の検定方法について学びました。この章では、2つの標本から得た標本比率を使って母比率が等しいかを検定する方法について学びます。
例題:
あるドラマの視聴率を調査したところ、関東地区では5,000世帯中1,000世帯が視聴していたことが分りました。一方、関西地区では3,000世帯中540世帯が視聴していました。この結果から、2地区の視聴率に差があるといえるでしょうか。
| 関東地区 | 関西地区 | |
|---|---|---|
| 調査世帯数 | 5000 | 3000 |
| 視聴世帯数 | 1000 | 540 |
- 仮説を立てる
- 有意水準を設定する
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説![]() は「関東地区と関西地区の視聴率は等しい」とします。したがって、対立仮説
は「関東地区と関西地区の視聴率は等しい」とします。したがって、対立仮説![]() は「関東地区と関西地区の視聴率は等しくない(差がある)」となります。
は「関東地区と関西地区の視聴率は等しくない(差がある)」となります。
![]() とします。
とします。
母比率の差の検定では、サンプルサイズnが十分に大きい時には、次の式から得られる統計量zは標準正規分布![]() に従います。1群目の標本比率を
に従います。1群目の標本比率を![]() 、サンプルサイズを
、サンプルサイズを![]() 、2群目の標本比率を
、2群目の標本比率を![]() 、サンプルサイズを
、サンプルサイズを![]() とします。また、この式では2つの標本比率を1つにまとめた標本比率(プールした標本比率)
とします。また、この式では2つの標本比率を1つにまとめた標本比率(プールした標本比率)![]() を使います。
を使います。
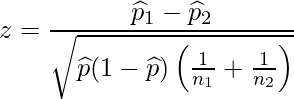
プールした標本比率![]() は次の式から求めます。
は次の式から求めます。
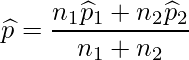
この検定で使用する分布は「標準正規分布」になります。また、関東地区と関西地区とで視聴率に差があるかどうかを確認したいので、両側検定を行います。統計数値表から![]() の値を読み取ると「1.96」となっています。
の値を読み取ると「1.96」となっています。
調査結果から標本比率![]() 、
、![]() 、プールした標本比率
、プールした標本比率![]() は次のようになります。
は次のようになります。
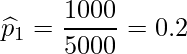
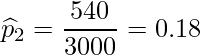
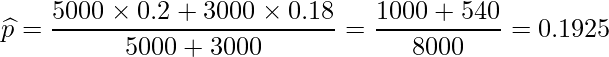
これらの標本比率とサンプルサイズを用いて統計量zを求めます。
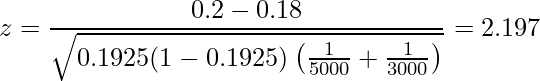
次の図は標準正規分布を表したものです。z=2.197は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において、帰無仮説![]() を棄却し、対立仮説
を棄却し、対立仮説![]() を採択する」という結果になります。つまり「関東地区と関西地区とで視聴率に差がある」と結論づけられます。
を採択する」という結果になります。つまり「関東地区と関西地区とで視聴率に差がある」と結論づけられます。
【コラム】母比率の差の検定と正規分布の再生性
正規分布の再生性については14-2章で既に学びました。確率変数![]() が二項分布
が二項分布![]() に従うとき、
に従うとき、![]() が大きい場合には
が大きい場合には![]() は正規分布
は正規分布![]() に従うので(21-1章)、これらの和(差)もまた正規分布に従います。
に従うので(21-1章)、これらの和(差)もまた正規分布に従います。
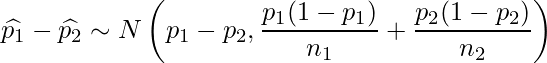
![]() を正規化した
を正規化した![]() は正規分布に従います。
は正規分布に従います。
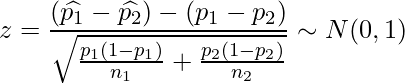
この母比率の差の検定は、帰無仮説![]() を
を![]() としていることから、
としていることから、![]() としたときの
としたときの![]() と
と![]() をプールした標本比率
をプールした標本比率![]() を使って、次のように書き換えられます。
を使って、次のように書き換えられます。
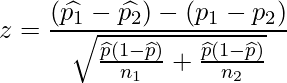
したがって、
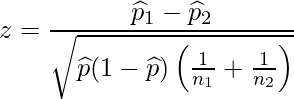
となります。
25. さまざまな検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
- 21. 母比率の区間推定
21-2. 母比率の信頼区間の求め方2
- 25. さまざまな検定
25-1. 母比率の検定
- 統計Tips
2群の母比率の差の検定
- ブログ
割合と比率
- ブログ
二項検定
- ブログ
2群の比率の差の検定
- ブログ
幾つデータが必要か? - 比率の差の検定