- Step1. 基礎編
- 30. 二元配置分散分析
30-3. 二元配置分散分析の分散分析表3
二元配置分散分析も一元配置分散分析と同じように、「平均平方」の比を用いて検定を行います。平均平方の比は不偏分散の比と同様にF分布を用いて検定できます。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | 126.64 | 3 | 42.21 | 29.49 |
| 土の種類 | 66.33 | 1 | 66.33 | 46.33 |
| 肥料の量×土の種類 | 17.79 | 3 | 5.93 | 4.14 |
| 残差 | 22.91 | 16 | 1.43 | |
| 全体 | 233.67 | 23 |
■F値について
統計量Fは「各因子の平均平方」を「残差の平均平方」で割って算出します。
肥料の量:42.21/1.43=29.49
土の種類:66.33/1.43=46.33
肥料の量×土の種類:5.93/1.43=4.14
■分散分析におけるF検定について
分散分析では測定誤差などによって生じる誤差(偶然誤差)のバラつき(=残差の平均平方)と比較して、データ全体の平均値から因子の各水準の平均値のズレ(=因子の平均平方)が十分に大きいかどうかを検定します。この検定により有意な結果となった場合、「データ全体の平均値から因子の各水準の平均値のズレが偶然誤差よりも有意に大きい=因子の水準間の平均値には差がある」と結論付けられます。
分散分析表の統計量Fの値を、F分布を使って検定した結果が次の表です。有意水準は5%です。
| 因 子 | 使用する F分布の自由度 |
F分布表から 読み取ったF値 |
分散分析から得られた 統計量Fの値 |
検定結果 |
|---|---|---|---|---|
| 肥料の量 | (3, 16) | 3.239 | 29.49 | 帰無仮説を棄却 |
| 土の種類 | (1, 16) | 4.494 | 46.33 | 帰無仮説を棄却 |
| 肥料の量×土の種類 | (3, 16) | 3.239 | 4.14 | 帰無仮説を棄却 |
いずれの因子の統計量Fも、有意水準5%ではF分布表から読み取ったF値と比較して大きくなっています。つまり、いずれの因子の統計量FにおいてもF統計分布の棄却域に入っていることから、有意水準5%の片側検定において帰無仮説![]() を棄却し、対立仮説
を棄却し、対立仮説![]() を採択します。言い換えると「肥料の量によって収量の平均値に差がある」および「土の種類によって収量の平均値に差がある」と結論付けられます。ここでは「肥料の量×土の種類」の「交互作用」について考えていません。交互作用を含めた結論については次の30-4章で説明します。
を採択します。言い換えると「肥料の量によって収量の平均値に差がある」および「土の種類によって収量の平均値に差がある」と結論付けられます。ここでは「肥料の量×土の種類」の「交互作用」について考えていません。交互作用を含めた結論については次の30-4章で説明します。
■各水準の母平均の信頼区間
因子AとBの交互作用が有意である場合、Aにおける水準![]() かつBにおける水準
かつBにおける水準![]() の母平均の信頼区間は次の式から求められます。
の母平均の信頼区間は次の式から求められます。
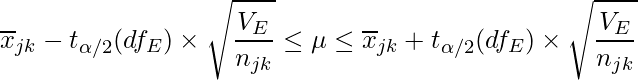
![]() は水準
は水準![]() の標本平均を、
の標本平均を、![]() は残差の自由度を、
は残差の自由度を、![]() は残差の平均平方を、
は残差の平均平方を、![]() は水準
は水準![]() におけるサンプルサイズを表します。
におけるサンプルサイズを表します。
例えば、29-2章の例題の「肥料 100g」かつ「土A」の作物の収量の母平均の95%信頼区間は
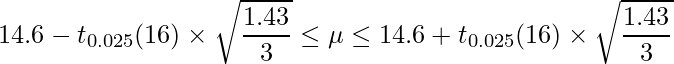
と計算できます。
因子AとBの交互作用が有意ではない場合、因子AとBを分けて考えます。Aにおける水準![]() 、Bにおける水準
、Bにおける水準![]() の母平均の信頼区間はそれぞれ次の式から求められます。
の母平均の信頼区間はそれぞれ次の式から求められます。
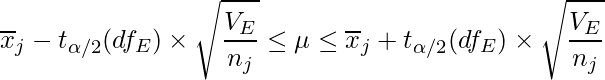
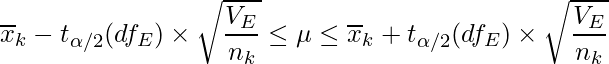
![]() と
と![]() は各水準
は各水準![]() と
と![]() の標本平均を、
の標本平均を、![]() は残差の自由度を、
は残差の自由度を、![]() は残差の平均平方を、
は残差の平均平方を、![]() と
と![]() は水準
は水準![]() と
と![]() におけるサンプルサイズを表します。
におけるサンプルサイズを表します。
30. 二元配置分散分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 29. 一元配置分散分析
29-4. 一元配置分散分析の流れ3
- 統計解析事例
二元配置分散分析─エクセル統計による解析事例
- ブログ
エクセル統計の分散分析について
- ブログ
交互作用とは
- ブログ
ANOVA と GLM







