- Step1. 基礎編
- 30. 二元配置分散分析
30-5. 交互作用とは
この章では、「肥料の量×土の種類」で示される「交互作用(Interaction)」について説明します。交互作用は2つの因子が組み合わさることで初めて現れる相乗効果のことです。「肥料の量×土の種類」の場合、肥料の量と土の種類が相互に影響を及ぼし合っていることを表します。また、交互作用による効果のことを「交互作用効果」といいます。
交互作用に対して、1つの因子に絞った場合の効果(この場合は肥料の量や土の種類のこと)のことを「主効果」といいます。
■交互作用図
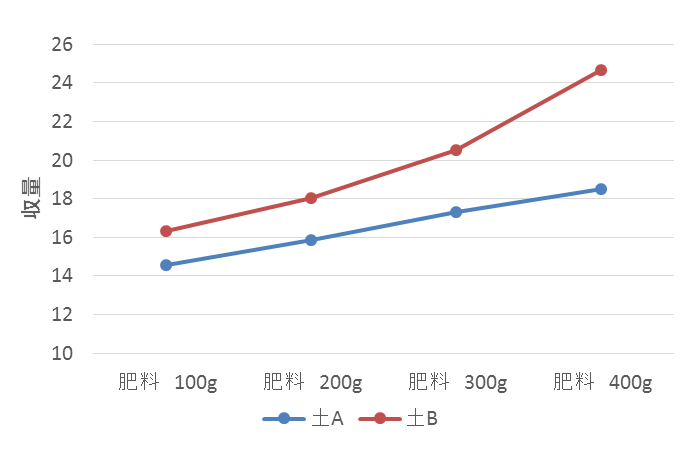
「肥料の量×土の種類」の「交互作用」を理解するにあたって、まず「土の種類」ごとに「収量の平均値」の折れ線グラフを描きます。横軸は「肥料の量」です。このグラフは「交互作用図」とよばれます。
逆に、次のグラフのように「肥料の量」ごとに「収量の平均値」の折れ線を描いても問題ありません。この場合の横軸は「土の種類」です。
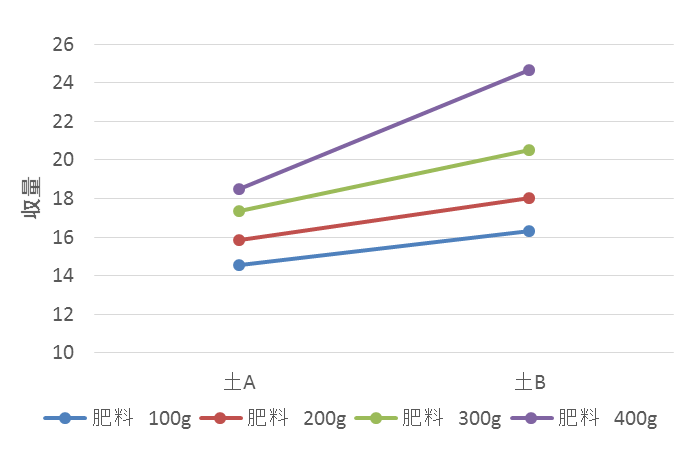
■交互作用効果
「土の種類」ごとの「収量の平均値」の折れ線グラフを見ると、土Aも土Bも肥料の量が増えるに連れて収量が増えていますが、土Bのほうが収量の伸びが大きいことが分かります。この伸びは、肥料の量の増加に加えて土の種類の影響によるものだと考えられます。このように、土の種類によって肥料の量に対する収量の変化が異なっていることを「交互作用効果」といいます。
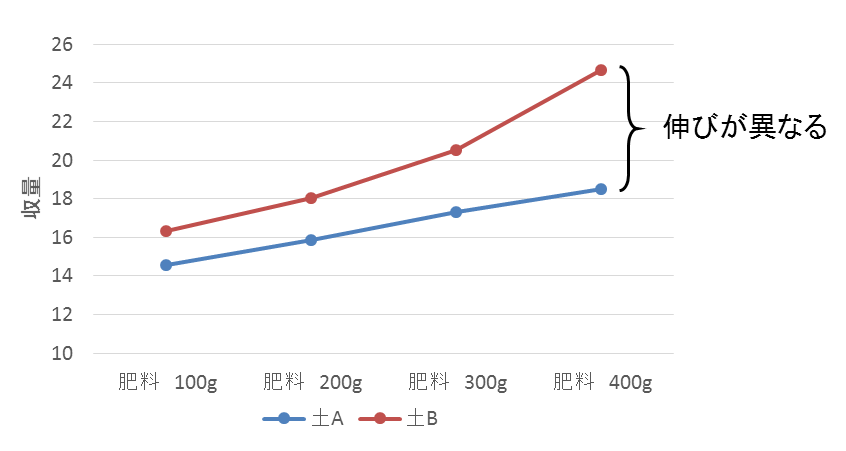
「肥料の量」ごとの「収量の平均値」の折れ線グラフの場合も同様に、肥料の量によって土の種類に対する収量の変化が異なっていることが分かります。
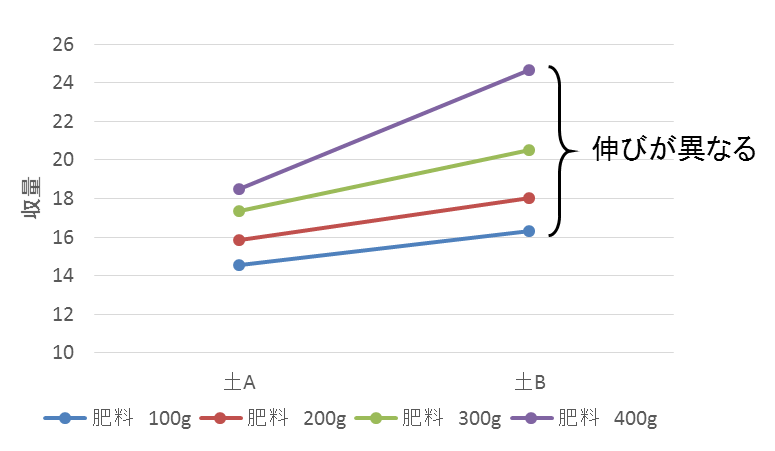
■交互作用が有意である場合
「交互作用効果」があるかどうかを検定した結果が、分散分析表の交互作用の行です。この交互作用の帰無仮説![]() は「肥料の量と土の種類の組み合わせによる収量への影響はない(肥料の量と土の種類の交互作用効果はない)」です。
は「肥料の量と土の種類の組み合わせによる収量への影響はない(肥料の量と土の種類の交互作用効果はない)」です。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | 126.64 | 3 | 42.21 | 29.49 |
| 土の種類 | 66.33 | 1 | 66.33 | 46.33 |
| 肥料の量×土の種類 | 17.79 | 3 | 5.93 | 4.14 |
| 残差 | 22.91 | 16 | 1.43 | |
| 全体 | 233.67 | 23 |
30‐3章の二元配置分散分析の結果、「肥料の量×土の種類」の「交互作用」もまた他の因子と同様に「有意水準5%の片側検定において、帰無仮説![]() を棄却し、対立仮説
を棄却し、対立仮説![]() を採択する」という結果になりました。
を採択する」という結果になりました。
| 因 子 | 使用する F分布の自由度 |
F分布表から 読み取ったF値 |
分散分析から得られた F統計量の値 |
検定結果 |
|---|---|---|---|---|
| 肥料の量 | (3, 16) | 3.239 | 29.49 | 帰無仮説を棄却 |
| 土の種類 | (1, 16) | 4.494 | 46.33 | 帰無仮説を棄却 |
| 肥料の量×土の種類 | (3, 16) | 3.239 | 4.14 | 帰無仮説を棄却 |
この結果は「肥料の量によって、土の種類の収量への効果が異なる」ということを意味します。つまり「収量に対する肥料の量と土の種類の効果は一様ではない」と結論付けられます。
■交互作用が有意ではない場合
交互作用が有意ではない場合、交互作用図は次の折れ線グラフのように平行になります。これは、「肥料の量が増えるに連れて収量が増えるが、その増え方は土の種類によって変わらない」ということを意味します。グラフの高さの違いは「土の種類」の影響を表します。
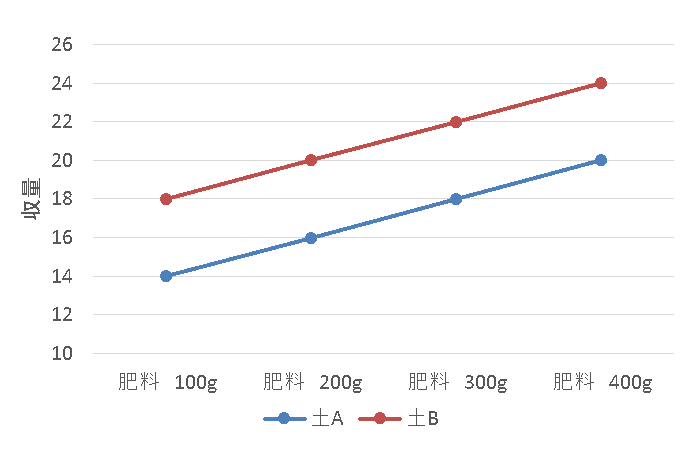
したがって、次の表のように交互作用が有意ではない結果が得られた場合には、因子ごとの結果のみを見ればよいことになります。つまり「肥料の量および土の種類の水準間で作物の収量の平均値に差がある」と結論付けられます。
| 因 子 | 検定結果 |
|---|---|
| 肥料の量 | 帰無仮説を棄却 |
| 土の種類 | 帰無仮説を棄却 |
| 肥料の量×土の種類 | 帰無仮説を棄却しない |
■おすすめ書籍
分散分析では多重比較を一緒に行うことが多いですが、いかんせんいろいろな種類があってよく分からない…という方も多いかもしれません。この本には、その数ある多重比較の各手法の理論や計算方法について詳しく掲載されています。
30. 二元配置分散分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
二元配置分散分析─エクセル統計による解析事例
- ブログ
エクセル統計の分散分析について
- ブログ
交互作用とは
- ブログ
ANOVA と GLM








