- 30. 二元配置分散分析
練習問題(30. 二元配置分散分析)
1
分散分析に関する記述のうち、正しいものはどれか。
- 分散分析は3群以上からなるデータにおいて、各群の母分散が異なるかどうかを検定する手法である。
- 一元配置分散分析を行う場合、各群のサンプルサイズが異なっていてもよい。
- 一元配置分散分析や二元配置分散分析では、交互作用の影響を見ることができる。
- 3つ以上の因子からなるデータを分散分析で分析することはできない。

答えを見る
- 答え
 閉じる
閉じる -
- ×:分散分析は3群以上からなるデータにおいて、各群の母平均の差を検定する手法です。
- ◯:正しいです。
- ×:交互作用は2つの因子が組み合わさることで初めて現れる相乗効果のことです。一元配置分散分析は1つの因子からなるデータの分析手法であるため、交互作用の影響を見ることはできません。
- ×:多元配置分散分析によって3つ以上の因子からなるデータを分析できます。
2
二元配置分散分析で分析できるデータはA、Bどちらか答えよ。
表A
| 肥料 100g | 肥料 200g | 肥料 300g | 肥料 400g | |
|---|---|---|---|---|
| 土A | 14.5 | 16.5 | 17.8 | 18.1 |
| 15.1 | 16.1 | 19 | 20.2 | |
| 14.1 | 15 | 15.2 | 17.2 | |
| 土B | 16.2 | 18.6 | 21.7 | 23.6 |
| 15.3 | 16.9 | 20.5 | 24.9 | |
| 17.5 | 18.6 | 19.4 | 25.5 |
表B
| 肥料 100g | 肥料 200g | 肥料 300g | 肥料 400g |
|---|---|---|---|
| 14.5 | 16.5 | 17.8 | 18.1 |
| 15.1 | 16.1 | 19 | 20.2 |
| 14.1 | 15 | 15.2 | 17.2 |
| 16.2 | 18.6 | 21.7 | 23.6 |
| 15.3 | 16.9 | 20.5 | 24.9 |
| 17.5 | 18.6 | 19.4 | 25.5 |

答えを見る
- 答え
 閉じる
閉じる -
答えは「表A」です。
二元配置分散分析では「要因」が二つ必要となります。表Aでは、「肥料を与えた量」と「土の種類」の二つの要因がありますが、表Bでは「肥料を与えた量」の一つの要因しかありません。したがって前者は二元配置分散分析で、後者は一元配置分散分析で分析できるデータです。
なお、二元配置というのはあくまで「要因」が二つであればよく、「水準」について特に制限はありません。「要因」と「水準」という用語を混同して覚えないように意識すると分かりやすくなります。
3
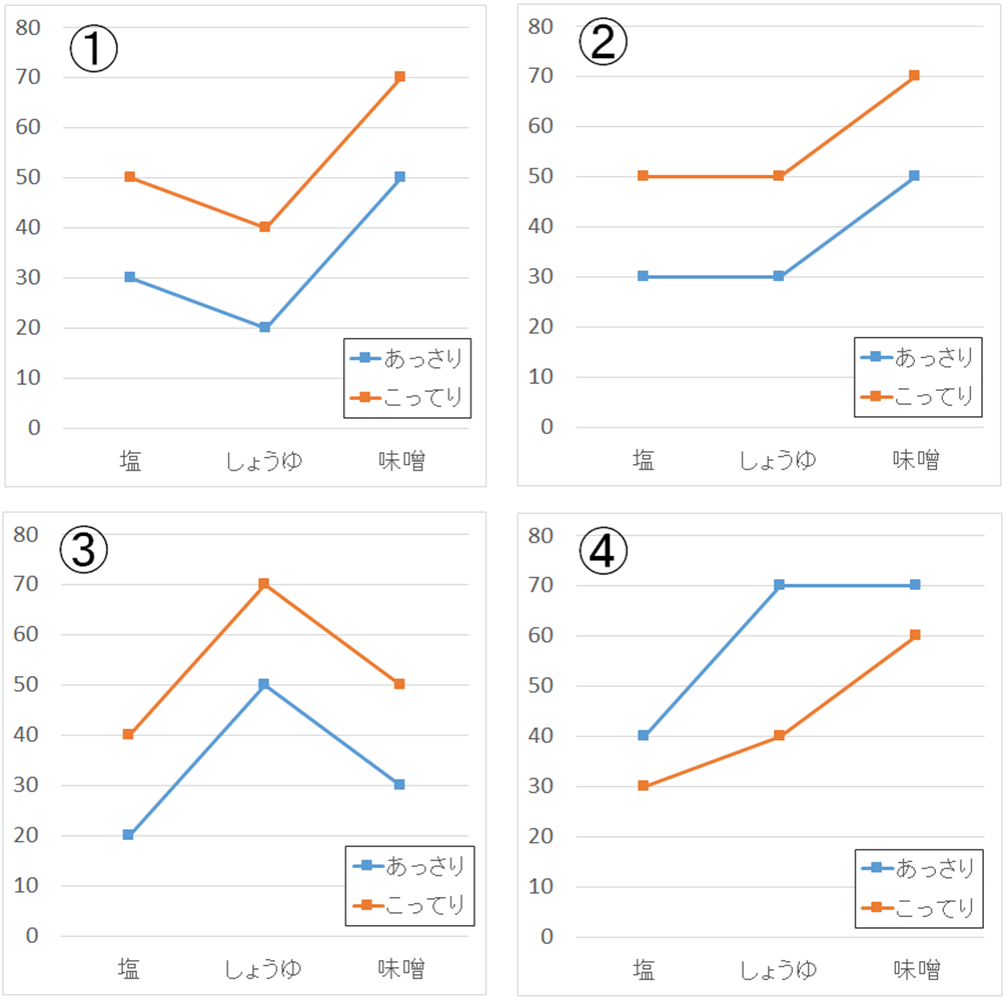
ラーメンのおいしさを定量化する実験を行い、結果を二元配置分散分析によって分析したところ、次のようなグラフが得られたとする。この4つのグラフのうち、交互作用があると考えられるものを選べ。

答えを見る
- 答え
 閉じる
閉じる -
答えは「4」のグラフです。
交互作用が認められる場合には、グラフの線が平行になりません。グラフの中で、どちらか一方の折れ線を縦に平行移動して形が一致しないものは4のグラフだけであることから、4の結果の場合には交互作用があると考えられます。
4
次の分散分析表の空欄AからFを埋めよ。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 要因A | 1250 | 5 | 250 | 5 |
| 要因B | 1750 | 5 | C | E |
| 要因A×要因B | 3750 | B | D | F |
| 残差 | A | 72 | 50 | |
| 全体 | 10350 | 107 |

答えを見る
- 答え
 閉じる
閉じる -
交互作用のある場合での二元配置分散分析表は、次のようなルールに従って計算できます。
- 全体の平方和=要因Aの平方和+要因Bの平方和+要因A×要因Bの平方和+誤差の平方和
- 全体の自由度=要因Aの自由度+要因Bの自由度+要因A×要因Bの自由度+誤差の自由度
- 平均平方=平方和÷自由度
- F値=各要因の平均平方÷誤差の平均平方
これらのルールを利用すると、表を埋めることが出来ます。まず、Aについては1.より「誤差の平方和=全体の平方和-(要因全ての平方和)」で計算できます。この式に具体的に数値をあてはめると、10350-(1250+1750+3750)=3600と求められます。
Bについては、2.より「要因A×要因Bの自由度=全体の自由度-(要因A×要因B以外の自由度)」で計算できます。この式に具体的に数値をあてはめると、107-(5+5+72)=25と求められます。
C、Dについては3.より「要因の平均平方=要因の平方和÷要因の自由度」で計算できます。この式に具体的に数値をあてはめると、それぞれ1750÷5=350、3750÷25=150と求められます。
E、Fについては、4.を用いてそれぞれ350÷50=7、150÷50=3と計算できます。 以上をまとめると、答えは「A=3600 B=25 C=350 D=150 E=7 F=3」となります。
5
あるデータから二元配置分散分析を行ったところ、次の分散分析表を得た。この結果からのどのような解釈ができるか。ただし有意水準は5%とする。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 | P 値 |
|---|---|---|---|---|---|
| 要因A | 571.9 | 2 | 285.9 | 40.4 | p<0.001 |
| 要因B | 584.1 | 2 | 292.0 | 41.3 | p<0.001 |
| 要因A×要因B | 75.9 | 4 | 19.0 | 2.7 | 0.0648 |
| 残差 | 127.4 | 18 | 7.1 | ||
| 全体 | 1359.2 | 26 |

答えを見る
- 答え
 閉じる
閉じる -
二元配置分散分析では、まず交互作用が有意かどうかを確認します。この分散分析表を見ると有意ではないことが分かります。
交互作用が有意ではない場合、次に各要因が有意かどうか確認します。要因Aも要因Bも有意であることから、要因A間および要因B間において母平均に差があると言えます。
※各要因の効果が有意であった場合、その要因の中で具体的にどの群とどの群の間で差があったのかを確認するために「多重比較」を行います。







