- Step1. 基礎編
- 30. 二元配置分散分析
30-2. 二元配置分散分析の分散分析表2
この章では交互作用と残差、平均平方について説明します。30-1までの分散分析表はこちらになります。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | 126.64 | 3 | ||
| 土の種類 | 66.33 | 1 | ||
| 肥料の量×土の種類 | ||||
| 残差 | ||||
| 全体 | 233.67 | 23 |
■交互作用について
- 肥料の量×土の種類(交互作用)
- 交互作用(肥料の量×土の種類)の自由度
「肥料の量×土の種類」は、「肥料の量」や「土の種類」だけでは説明できない効果のことで、2つの因子が組み合わさることで初めて現れる効果です。一元配置分散分析では因子が1つしか無いため、交互作用について考える必要はありませんでした。詳細については30-4章で説明します。
「肥料の量×土の種類の平方和」は「データ全体の平均値からの肥料の量×土の種類の平均値のズレ」を求め、「データ全体の平均値からの肥料の量の各水準の平均値のズレ」と「全体の平均値からの土の種類の各水準の平均値のズレ」を引いたものです。
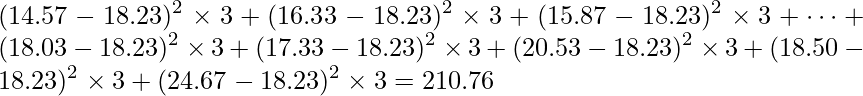
「交互作用(肥料の量×土の種類)の自由度」は2つの因子の水準数から1を引いたものをかけあわせたものになります。したがって「(4-1)×(2-1)=3」になります。
■残差について
「残差の平方和」は「全体の平方和」から「肥料の量の平方和」、「土の種類の平方和」、「肥料の量×土の種類(交互作用)の平方和」を引いたものになります。
「残差の自由度」は「全体の自由度」から「肥料の量の自由度」、「土の種類の自由度」、「肥料の量×土の種類(交互作用)の自由度」を引いたものになります。したがって「23-3-1-3=16」になります。
■平均平方について
最後に「平均平方」を求めます。平均平方は「平方和」を「自由度」で割ったもので、「全体」以外の因子について求めます。
肥料の量:126.64/3=42.21
土の種類:66.33/1=66.33
肥料の量×土の種類:17.79/3=5.93
残差:22.91/16=1.43
これらの値を分散分析表に入れると次のようになります。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | 126.64 | 3 | 42.21 | |
| 土の種類 | 66.33 | 1 | 66.33 | |
| 肥料の量×土の種類 | 17.79 | 3 | 5.93 | |
| 残差 | 22.91 | 16 | 1.43 | |
| 全体 | 233.67 | 23 |
30. 二元配置分散分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 29. 一元配置分散分析
29-3. 一元配置分散分析の流れ2
- 29. 一元配置分散分析
29-4. 一元配置分散分析の流れ3
- 統計解析事例
二元配置分散分析─エクセル統計による解析事例
- ブログ
エクセル統計の分散分析について
- ブログ
交互作用とは
- ブログ
ANOVA と GLM







