- Step1. 基礎編
- 30. 二元配置分散分析
30-1. 二元配置分散分析の分散分析表1
二元配置分散分析は因子を2つ含むデータから、各因子における水準間の平均値の差を検定するための分析方法です。
例題:
下の表はある作物の収量(kg)についてまとめたものです。肥料の量4パターンと、土をAとBの2種類を用いて、計8通りの生育環境において各3回の実験を行いました。このデータから、各因子(肥料の量、および土の種類)の水準間で収量の平均値に差があるかどうかを二元配置分散分析で検定します。帰無仮説![]() は「各因子の水準間で作物の収量の平均値は等しい」とします。
は「各因子の水準間で作物の収量の平均値は等しい」とします。
| 肥料 100g | 肥料 200g | 肥料 300g | 肥料 400g | |
|---|---|---|---|---|
| 土A | 14.5 | 16.5 | 17.8 | 18.1 |
| 15.1 | 16.1 | 19 | 20.2 | |
| 14.1 | 15 | 15.2 | 17.2 | |
| 土B | 16.2 | 18.6 | 21.7 | 23.6 |
| 15.3 | 16.9 | 20.5 | 24.9 | |
| 17.5 | 18.6 | 19.4 | 25.5 |
二元配置分散分析も一元配置分散分析と同じく、ポイントは「データ全体の平均値から因子の各水準の平均値がどのくらいずれているか」を見ることです。上のデータのように1種類の条件で複数回実験を行ったデータの場合(ここでは8通りの生育環境それぞれで3回の実験を実施)、一元配置分散分析とは異なり「交互作用」の有無についても解析することができます。交互作用については30‐4章で詳しく説明します。
二元配置分散分析の分散分析表は次のような形です。「肥料の量×土の種類」が交互作用を表しています。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | ||||
| 土の種類 | ||||
| 肥料の量×土の種類 | ||||
| 残差 | ||||
| 全体 |
■平均値について
この分散分析表を埋めるために、まずさまざまな平均値を求めます。
- 【全体】すべてのデータの平均値:18.23
- 【肥料の量ごとの平均値】肥料100g:15.45、肥料200g:16.95、肥料300g:18.93、肥料400g:21.58
- 【土の種類ごとの平均値】土A:16.57、土B:19.89
- 【肥料の量と土の種類ごとの平均値】肥料100g×土A:14.57、肥料100g×土B:16.33、肥料200g×土A:15.87、肥料200g×土B:18.03、肥料300g×土A:17.33、肥料300g×土B:20.53、肥料400g×土A:18.50、肥料400g×土B:24.67
■平方和について
- 全体の平方和
- 肥料の量の平方和
- 土の種類の平方和
「全体の平方和」は「データ全体の平均値からの各データのズレ」を求めたものです。
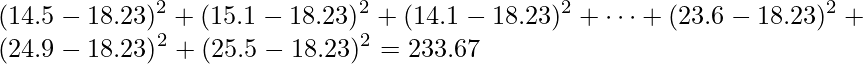
「肥料の量の平方和」は「データ全体の平均値からの肥料の量の各水準の平均値のズレ」を求めたものです。
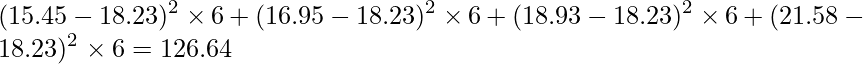
「土の種類の平方和」は「全体の平均値からの土の種類の各水準の平均値のズレ」を求めたものです。
■自由度について
- 全体の自由度
- 肥料の量の自由度
- 土の種類の自由度
「全体の自由度」は全てのデータの個数から1を引いたものになります。したがって「24-1=23」になります。
「肥料の量の自由度」は肥料の量の水準数から1を引いたものになります。したがって「4-1=3」になります。
「土の種類の自由度」は土の種類の水準数から1を引いたものになります。したがって「2-1=1」になります。
これらの値を分散分析表に入れると次のようになります。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | 126.64 | 3 | ||
| 土の種類 | 66.33 | 1 | ||
| 肥料の量×土の種類 | ||||
| 残差 | ||||
| 全体 | 233.67 | 23 |
■おすすめ書籍
二元配置分散分析もこちらの本でバッチリ勉強できます!
30. 二元配置分散分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 29. 一元配置分散分析
29-1. 分散分析とは
- 29. 一元配置分散分析
29-3. 一元配置分散分析の流れ2
- 統計解析事例
二元配置分散分析─エクセル統計による解析事例
- ブログ
エクセル統計の分散分析について
- ブログ
交互作用とは
- ブログ
ANOVA と GLM







