- Step1. 基礎編
- 25. さまざまな検定
25-1. 母比率の検定
前章で学んだ平均値の検定では、母集団が正規分布に従うことが必要な条件でした。しかし、母集団が正規分布に従わない場合でも、標本が十分に大きい場合には標本平均の分布は正規分布に従うことから(中心極限定理)、標準正規分布を用いて検定を行うことができます。
例題:
あるサイコロを12,000回投げたときに1が2,200回出ました。このサイコロはどの目も等しく出る歪みのないサイコロといえるでしょうか。

- 仮説を立てる
- 有意水準を設定する
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説![]() は「このサイコロは歪みのないもので、1が出る確率は1/6(=0.167)である」とします。したがって、対立仮説
は「このサイコロは歪みのないもので、1が出る確率は1/6(=0.167)である」とします。したがって、対立仮説![]() は「このサイコロは歪んでいて、1が出る確率は1/6ではない」となります。
は「このサイコロは歪んでいて、1が出る確率は1/6ではない」となります。
一般的に、帰無仮説としては「現在の状態を表す(何らかの事象や現象が生じていないことを仮定する)仮説」を、対立仮説には「新しい状態を表す(何らかの事象や現象が生じたと仮定する)仮説」を設定します。
![]() とします。
とします。
母比率の検定では、サンプルサイズnが十分に大きい時には、次の式から得られる統計量zは標準正規分布N(0, 1)に従います。![]() は標本比率、
は標本比率、![]() は母比率を表します。
は母比率を表します。
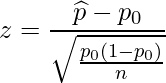
この検定で使用する分布は「標準正規分布」になります。また、サイコロの1の目の出方に歪みがないかどうかを確認したいので、両側検定を行います。統計数値表から![]() の値を読み取ると「1.96」となっています。
の値を読み取ると「1.96」となっています。
サイコロを投げた結果から標本比率![]() は次のようになります。
は次のようになります。
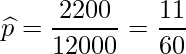
この標本比率と母比率![]() =1/6、サンプルサイズn=12,000を用いて、統計量zを求めます。
=1/6、サンプルサイズn=12,000を用いて、統計量zを求めます。
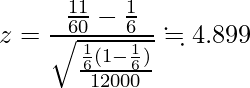
次の図は標準正規分布を表したものです。z=4.899は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において、帰無仮説![]() を棄却し、対立仮説
を棄却し、対立仮説![]() を採択する」という結果になります。つまり「このサイコロの1が出る確率は1/6ではない、すなわちこのサイコロは1の出やすさに関して歪んでいる」と結論づけられます。
を採択する」という結果になります。つまり「このサイコロの1が出る確率は1/6ではない、すなわちこのサイコロは1の出やすさに関して歪んでいる」と結論づけられます。

25. さまざまな検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
- 21. 母比率の区間推定
21-2. 母比率の信頼区間の求め方2
- 統計Tips
2群の母比率の差の検定
- ブログ
割合と比率
- ブログ
二項検定
- ブログ
2群の比率の差の検定
- ブログ
幾つデータが必要か? - 比率の差の検定






