- Step1. 基礎編
- 15. いろいろな確率分布3
15-6. 2変数の期待値と分散
12-3章では確率変数の期待値について、12-5章では確率変数の分散について学びました。この章では、2つの確率変数の和、差、共分散、相関係数について学びます。
■2つの確率変数の期待値
2つの確率変数![]() とYの和
とYの和![]() 、差
、差![]() の期待値は、次に示すように
の期待値は、次に示すように![]() 、
、![]() それぞれの期待値
それぞれの期待値![]() 、
、![]() の和、差に等しくなります。
の和、差に等しくなります。
例えば、2つのさいころの出る目![]() 、
、![]() の和の期待値
の和の期待値![]() は、次のように計算できます。
は、次のように計算できます。
![]() と
と![]() が独立である場合には、次の式が成り立ちます。
が独立である場合には、次の式が成り立ちます。
■2つの確率変数の分散
一方、2つの確率変数![]() とYの和
とYの和![]() 、差
、差![]() の分散は次に示すように、必ずしも
の分散は次に示すように、必ずしも![]() 、
、![]() それぞれの分散
それぞれの分散![]() 、
、![]() の和に等しくなるわけではありません。
の和に等しくなるわけではありません。
ここで示した![]() は共分散です。共分散が0、すなわち
は共分散です。共分散が0、すなわち![]() と
と![]() が独立である場合には次の式が成り立ちます。この場合、確率変数の和の分散も差の分散もそれぞれの確率変数の分散の和に等しくなります。
が独立である場合には次の式が成り立ちます。この場合、確率変数の和の分散も差の分散もそれぞれの確率変数の分散の和に等しくなります。
■2つの確率変数の共分散
共分散とは2変数の関係の強さを表す指標の一つで、![]() (Covariance)で表されます。確率変数
(Covariance)で表されます。確率変数![]() 、
、![]() の期待値をそれぞれ
の期待値をそれぞれ![]() 、
、![]() とすると、
とすると、![]() と
と![]() の共分散
の共分散![]() は次の式から計算できます。
は次の式から計算できます。
この式を展開すると、次のようになります。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle Cov(X,Y)&=&E[(X-\mu_x)(Y-\mu_y)] \\ &=&E(XY-\mu_xY-\mu_yX+\mu_x\mu_y) \\ &=&E(XY)-\mu_xE(Y)-\mu_yE(X)+\mu_x\mu_y \\ &=&E(XY)-\mu_x\mu_y-\mu_x\mu_y+\mu_x\mu_y \\ &=&E(XY)-\mu_x\mu_y \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-eede6671541630710ff6a784f3975092_l3.png)
![]() と
と![]() に正の相関がある場合には
に正の相関がある場合には![]() に、負の相関がある場合には
に、負の相関がある場合には![]() になります。上に挙げた和の分散の式は展開すると、
になります。上に挙げた和の分散の式は展開すると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V(X+Y)&=&E[\left\{(X+Y)-(\mu_x+\mu_y)\right\}^2] \\ &=&E[(X-\mu_x)^2+(Y-\mu_y)^2+2E(X-\mu_x)(Y-\mu_y)] \\ &=&V(X)+V(Y)+2E[(X-\mu_x)(Y-\mu_y)] \\ &=&V(X)+V(Y)+2Cov(X,Y) \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-394dc9551f9f52b15b801671dc8dd8d1_l3.png)
となることからも確認できます。共分散を使うと2つの確率変数![]() と
と![]() の相関係数
の相関係数![]() を計算できます。相関係数は
を計算できます。相関係数は![]() と
と![]() の共分散
の共分散![]() をそれぞれの標準偏差で割ったものであることは26-3章で既に学びました。
をそれぞれの標準偏差で割ったものであることは26-3章で既に学びました。
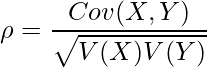
例題:
次の表はAさん、Bさん、Cさんの国語の点数![]() と数学の点数
と数学の点数![]() をまとめたものです。
をまとめたものです。![]() の期待値、
の期待値、![]() の分散、
の分散、![]() と
と![]() の相関係数を求めてみます。
の相関係数を求めてみます。
| Aさん | Bさん | Cさん | |
|---|---|---|---|
| 国語(X) | 40 | 50 | 60 |
| 数学(Y) | 70 | 50 | 90 |
| 合計(X+Y) | 110 | 100 | 150 |
![]() 、
、![]() です。したがって
です。したがって![]() の期待値は次のように計算できます。
の期待値は次のように計算できます。
また、![]() の分散は次のように計算できます。
の分散は次のように計算できます。
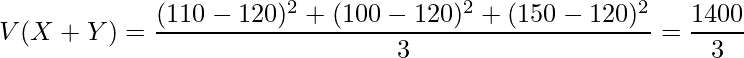
共分散の求め方は2通りあり、![]() を使うと、
を使うと、
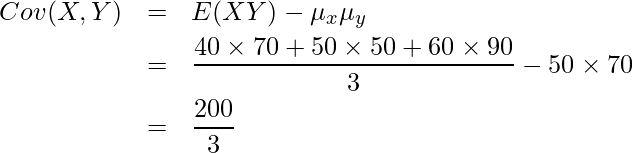
となります。一方、![]() を使う場合には、先に
を使う場合には、先に![]() と
と![]() を求めておきます。
を求めておきます。
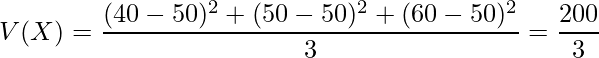
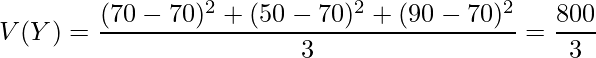
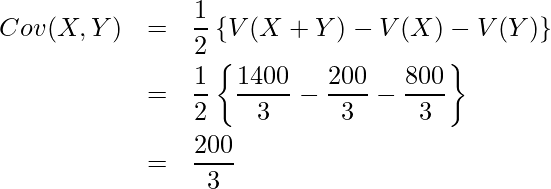
この共分散![]() を使うと相関係数
を使うと相関係数![]() は、
は、
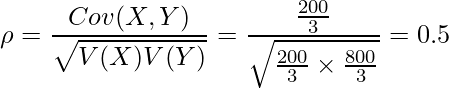
となります。







