- Step2. 中級編
- 8. 多変量解析
8-5. 階層型クラスター分析2
■サンプル間の距離計算方法
7-4章では、サンプル間の距離を計算するために「ユークリッド距離」を算出しました。距離計算には他にも様々な方法があります。ここではまず、クラスター分析で使われる距離計算方法について詳しく見てみます。
![]() 次元における2点、
次元における2点、![]() と
と ![]() の間の距離について考えます。
の間の距離について考えます。
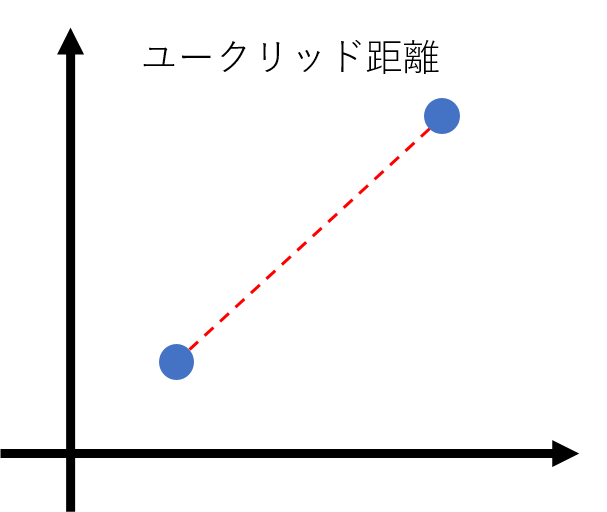
- ユークリッド距離
2点間の直線距離のことで、最も一般的な距離計算方法です。![]() と
と ![]() の間のユークリッド距離は次の式から算出できます。
の間のユークリッド距離は次の式から算出できます。
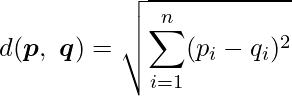
各次元における値の単位が異なる場合には、標準偏差 ![]() を使って2点間のユークリッド距離(標準化ユークリッド距離)を計算します。
を使って2点間のユークリッド距離(標準化ユークリッド距離)を計算します。
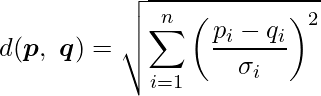
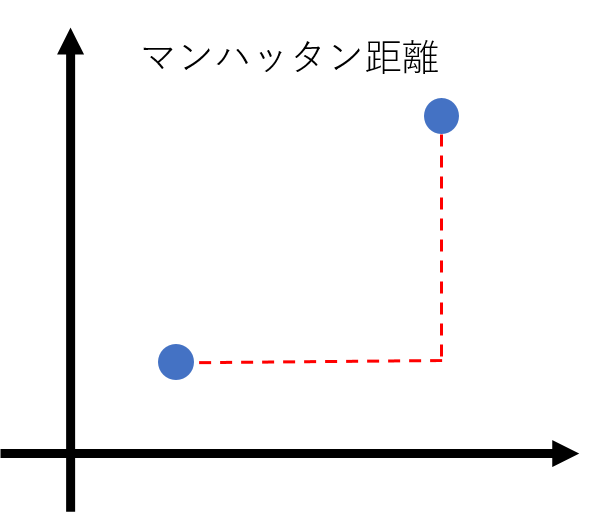
碁盤の目の街を歩いたときの最短距離のことで、![]() と
と ![]() の各次元における距離を計算しその和をとったものになります。
の各次元における距離を計算しその和をとったものになります。
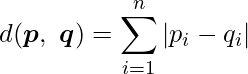
![]() を任意の整数とするとき、ミンコフスキー距離は次の式から算出できます。ユークリッド距離やマンハッタン距離を一般化したものになります。
を任意の整数とするとき、ミンコフスキー距離は次の式から算出できます。ユークリッド距離やマンハッタン距離を一般化したものになります。
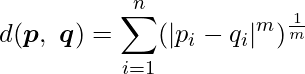
この式から分かるように、![]() のときにはユークリッド距離となり、
のときにはユークリッド距離となり、![]() のときにはマンハッタン距離となります。
のときにはマンハッタン距離となります。
サンプル間の相関関係を考慮した距離計算方法で、![]() と
と ![]() の間のマハラノビス距離は次の式から算出できます。異常データを検知する際に使われる場合があります。
の間のマハラノビス距離は次の式から算出できます。異常データを検知する際に使われる場合があります。
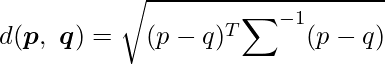
![]() は分散共分散行列を表します。
は分散共分散行列を表します。
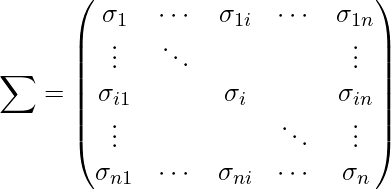
また、![]() は
は ![]() の逆行列を表します。
の逆行列を表します。
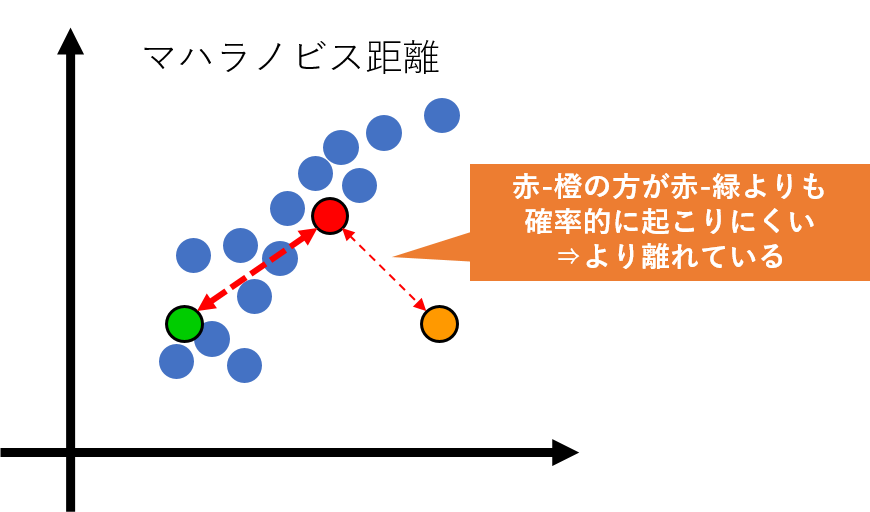
この図から分かるように、マハラノビス距離では確率的に起こりにくい=距離がより離れている=より異常な値であると見なします。
各次元における差の絶対値を算出し、その中から最大となるものが2点間のチェビシェフ距離です。

■クラスター間の距離計算方法
次に、クラスター間の距離算出方法について詳しく見てみます。7-4章で用いた「重心法」以外にもにもさまざまな距離計算方法が用いられます。
![]() からなるクラスター
からなるクラスター ![]() と
と![]() からなるクラスター
からなるクラスター ![]() の間の距離
の間の距離 ![]() について考えます。
について考えます。
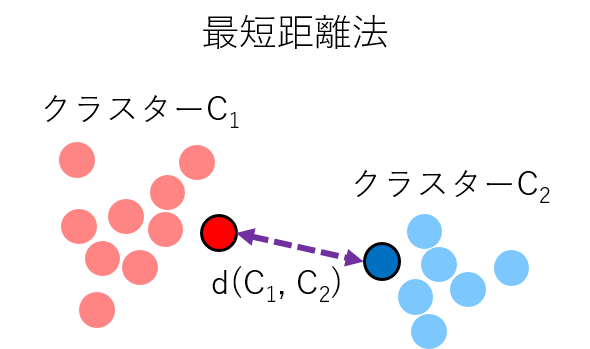
- 最短距離法
- メリット:計算量が少ない
- デメリット:分類感度が低い。外れ値に弱い、鎖効果(クラスターが帯状になる現象のこと)が出やすい
各クラスター内のサンプル間の距離のうち、最も距離が短いものをクラスター間の距離とする方法です。
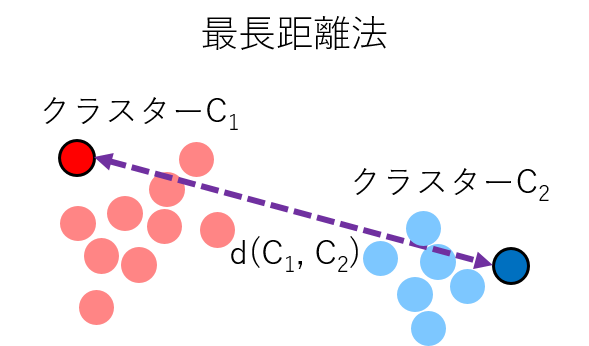
各クラスター内のサンプル間の距離のうち、最も距離が長いものをクラスター間の距離とする方法です。
- メリット:計算量が少ない
- デメリット:外れ値に弱い、拡散効果(本当は距離が近いクラスターが結合しない現象のこと)が出やすい
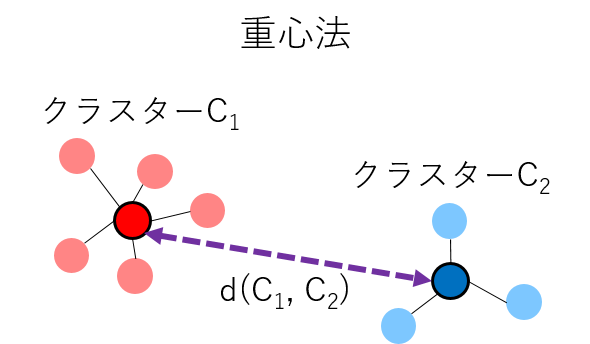
各クラスター内のサンプルの重心を算出し、重心間の距離をクラスター間の距離とする方法です。
- メリット:計算量が比較的少ない
- デメリット:-
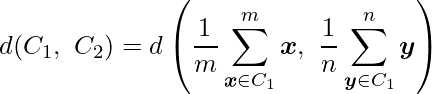
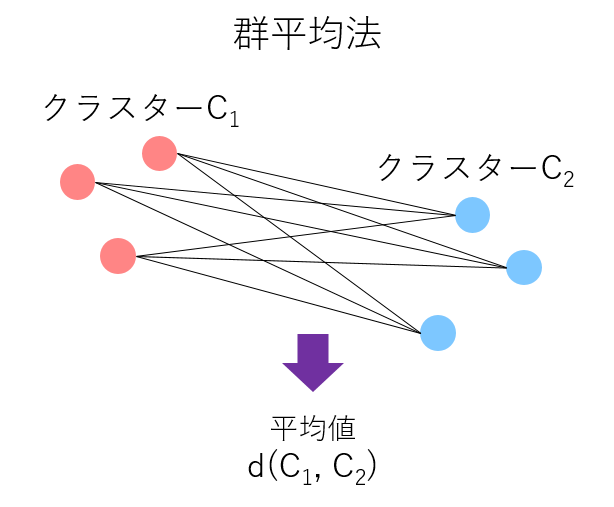
各クラスター内のサンプル間の距離を算出し、すべての距離の平均値をクラスター間の距離とする方法です。
- メリット:計算量が比較的少ない、鎖効果や拡散効果が出にくい
- デメリット:-
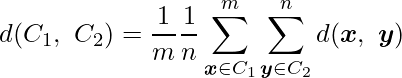
2つのクラスターを結合した後のクラスター内サンプルの重心から各サンプルまでの距離の二乗和(![]() の部分)から、結合前の2つのクラスター内サンプルの重心から各サンプルまでの二乗和(
の部分)から、結合前の2つのクラスター内サンプルの重心から各サンプルまでの二乗和(![]() と
と ![]() の部分)を引いた値をクラスター間の距離とする方法です。
の部分)を引いた値をクラスター間の距離とする方法です。
- メリット:分類感度が高いため、クラスター分析で非常によく用いられる
- デメリット:計算量が多い
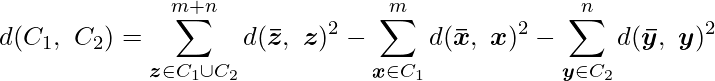
8. 多変量解析
- 8-1. ロジスティック回帰分析1
- 8-2. ロジスティック回帰分析2
- 8-3. ロジスティック回帰分析3
- 8-4. 階層型クラスター分析1
- 8-5. 階層型クラスター分析2
- 8-6. 非階層型クラスター分析







