- Step2. 中級編
- 8. 多変量解析
8-1. ロジスティック回帰分析1
ロジスティック回帰分析は、目的変数が0と1からなる2値のデータ、あるいは0から1までの値からなる確率などのデータについて、説明変数を使った式で表す方法のことです。ロジスティック回帰分析を行うと、説明変数を用いてある事象が起こる確率を予測することができます。
目的変数が0/1からなる2値データ ![]() が
が ![]() となる確率を
となる確率を ![]() 、
、![]() 個の説明変数
個の説明変数 ![]() をそれぞれ
をそれぞれ ![]() 、偏回帰係数をそれぞれ
、偏回帰係数をそれぞれ ![]() とすると、ロジスティック回帰モデルは次の式で表すことができます。
とすると、ロジスティック回帰モデルは次の式で表すことができます。
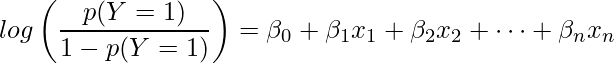
このとき、![]() を
を ![]() に変換することで、0から1の間の値しか取らない
に変換することで、0から1の間の値しか取らない ![]() を
を ![]() から
から ![]() までの値を取る連続データに変換することができます。
までの値を取る連続データに変換することができます。
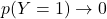 のとき
のとき 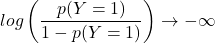
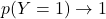 のとき
のとき 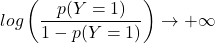
ロジット変換により目的変数が取りうる値に制約がなくなるため、線形モデルとして偏回帰係数を推定することができます。
■ロジット変換とロジスティック変換
0/1からなる2値データ ![]() が
が ![]() となる確率を
となる確率を ![]() とおいたときに、発生確率
とおいたときに、発生確率 ![]() を対数オッズに変換することを「ロジット変換」といいます。また、対数オッズのことを「ロジット(logit)」といいます。
を対数オッズに変換することを「ロジット変換」といいます。また、対数オッズのことを「ロジット(logit)」といいます。
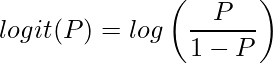
次に、ロジットの逆関数を計算してみます。![]() とおくと、
とおくと、
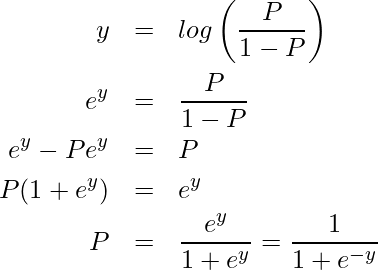
となります。ロジットの逆変換を「ロジスティック変換」といいます。また、![]() で表される関数のことを「ロジスティック関数」といいます。
で表される関数のことを「ロジスティック関数」といいます。

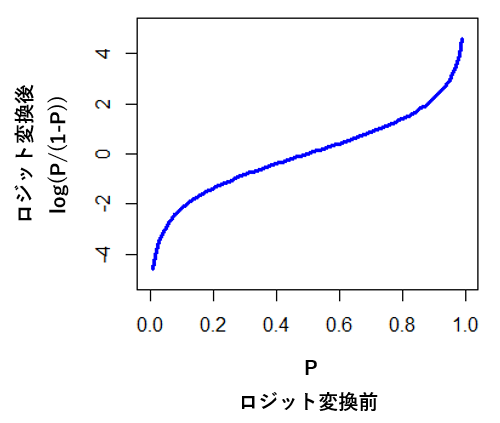
ロジスティック関数は「シグモイド関数」と呼ばれる場合もあります。この図から分かるように ![]() がどのような値をとっても、
がどのような値をとっても、![]() は0から1の間の値しか取りません。このシグモイド関数の特徴を用いて、線形モデルによる値が入力である場合に0から1の間の値として結果を出力するような回帰式を推定するのがロジスティック回帰分析です。
は0から1の間の値しか取りません。このシグモイド関数の特徴を用いて、線形モデルによる値が入力である場合に0から1の間の値として結果を出力するような回帰式を推定するのがロジスティック回帰分析です。
■ロジスティック回帰分析における偏回帰係数の推定
ロジスティック回帰分析における偏回帰係数の推定には最尤法を用います。最尤法とは、与えられた観測値から尤度を最大にするようなパラメーターを推定する方法のことで、最尤法によって推定された値を最尤推定値といいます。簡単に言うと、「いろいろなパラメーターの値を使ってある事象が起こる確率を計算してみて、一番確率が高くなったときにその値をパラメーターの推定値にする」という方法です。
2値データ ![]() が
が ![]() となる確率を
となる確率を ![]() 、
、![]() となる確率を
となる確率を ![]() とします。
とします。![]() 個のデータからなる
個のデータからなる ![]() が互いに独立であり
が互いに独立であり ![]() であるとき、尤度
であるとき、尤度 ![]() は次の式から計算できます。
は次の式から計算できます。
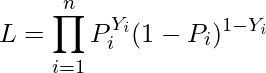
積のままだと計算がめんどくさいので、対数を取って和の形にします。これを対数尤度関数といいます。
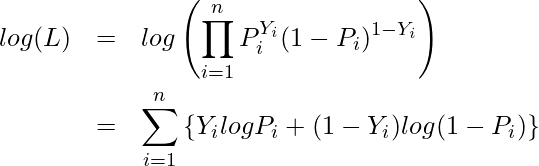
先程算出した式を対数尤度関数に代入し、対数尤度関数が最大となるように ![]() の値を計算します。
の値を計算します。
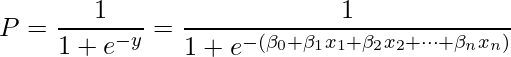
計算によって算出された ![]() を最尤推定量といいます。この計算にはニュートン=ラフソン法(ニュートン法)を使います。
を最尤推定量といいます。この計算にはニュートン=ラフソン法(ニュートン法)を使います。
発生確率の予測値は、算出した最尤推定量を用いて次のように計算できます。
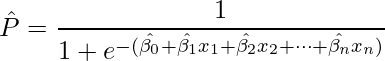
8. 多変量解析
- 8-1. ロジスティック回帰分析1
- 8-2. ロジスティック回帰分析2
- 8-3. ロジスティック回帰分析3
- 8-4. 階層型クラスター分析1
- 8-5. 階層型クラスター分析2
- 8-6. 非階層型クラスター分析







