- Step2. 中級編
- 8. 多変量解析
8-3. ロジスティック回帰分析3
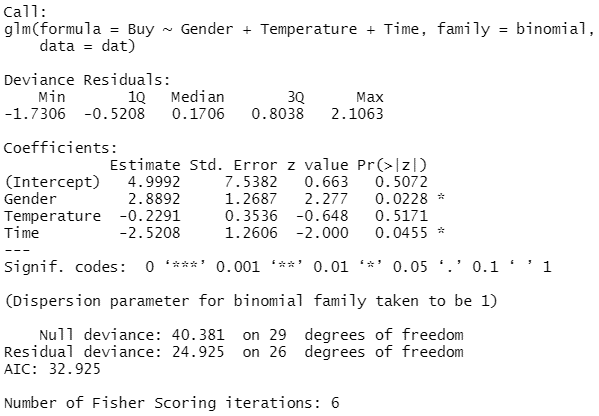
7-2章で得られたロジスティック回帰分析の結果をもう少し詳しく見てみます。
■予測値
推定された偏回帰係数を用いると、ある条件における事象の発生確率を予測することができます。7-1章で学んだように、![]() の発生確率
の発生確率 ![]() の予測値
の予測値 ![]() は算出した最尤推定量を用いて次のように計算できます。
は算出した最尤推定量を用いて次のように計算できます。
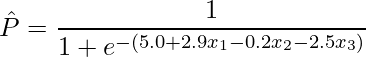
例えば「男性(![]() )・気温20℃(
)・気温20℃(![]() )・午前中(
)・午前中(![]() )」の場合、この式から飲料Aを購入する予測確率
)」の場合、この式から飲料Aを購入する予測確率 ![]() を計算すると
を計算すると
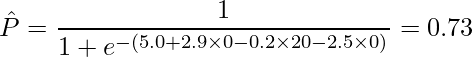
となります。
■モデルの適合度
データに対してロジスティック回帰分析によるモデル式が適合しているかどうかを確認する方法の1つに、「逸脱度(deviance)」を調べる方法があります。逸脱度は「-2×(対数尤度)」で定義されるものであり、逸脱度が大きいほど「あてはまりの悪いモデル」であることを意味します。説明変数が増えるほど、逸脱度は小さくなります。
目的変数が0と1からなる2値のデータ、あるいは0から1までの値からなる確率などのデータに対してロジスティック回帰分析を行った場合の逸脱度は次の式から計算できます。
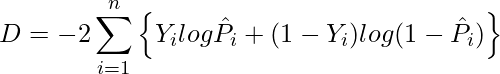
![]() は0/1からなる2値データ
は0/1からなる2値データ ![]() が
が ![]() となる確率
となる確率 ![]() の予測値を、
の予測値を、![]() は説明変数の数を表します。統計ソフトRによる解析結果の「Null deviance」は説明変数を1つも用いない場合のモデル(最も当てはまりの悪いモデル)の逸脱度を、「Residual deviance」はすべての説明変数を用いた場合のモデル(最も当てはまりの良いモデル)の逸脱度になります。
は説明変数の数を表します。統計ソフトRによる解析結果の「Null deviance」は説明変数を1つも用いない場合のモデル(最も当てはまりの悪いモデル)の逸脱度を、「Residual deviance」はすべての説明変数を用いた場合のモデル(最も当てはまりの良いモデル)の逸脱度になります。
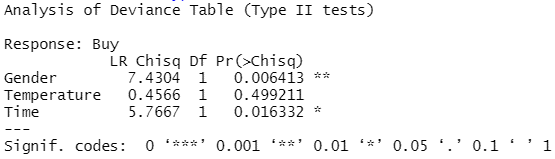
「LR(Likelihood Ratio)Chisq」は「その説明変数を含む場合の尤度」の「その説明変数を含まない場合の尤度」の比(尤度比)を表しています。この尤度比を用いてカイ二乗検定を行います。このモデルの検定結果を見ると、「Gender(性別)」と「Time(購入時間)」は有意な説明変数であるということが分かります。
モデルの適合度を調べる別の方法が「ホスマー=レメショウ検定(Hosmer-Lemeshow test)」です。逸脱度は、説明変数ごとにその説明変数がモデルにとって有意かどうかを調べるために使われますが、ホスマー=レメショウ検定は推定されたモデル式全体の適合度を調べるために使われます。
ホスマー=レメショウ検定では、まずデータを ![]() 個に分割します。この
個に分割します。この ![]() 個のグループを用いて、次の式からカイ二乗値を求めます。
個のグループを用いて、次の式からカイ二乗値を求めます。
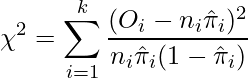
![]() は
は ![]() グループにおけるイベントの発生数を、
グループにおけるイベントの発生数を、![]() は
は ![]() グループにおけるサンプルの数を、
グループにおけるサンプルの数を、![]() は
は ![]() グループにおけるイベントの予測発生確率の平均値を表します。このカイ二乗値
グループにおけるイベントの予測発生確率の平均値を表します。このカイ二乗値 ![]() が自由度
が自由度 ![]() のカイ二乗分布に従うことを利用して検定を行います。
のカイ二乗分布に従うことを利用して検定を行います。
■変数選択
回帰分析を行う際に、複数の説明変数の中から効率的に目的変数を説明できる説明変数を何らかの基準に従って選択する場合があります。これを「変数選択」といいます。あまりにも多くの説明変数を使ったモデルの場合、そのデータに対しては非常に当てはまりが良いものの、別のデータでは当てはまりがあまり良くないという汎用性の低いモデルになってしまう場合があります。このような状態を「過剰適合(オーバーフィッティング)」といいます。
モデルの中から基準を満たす変数がなくなった時点で、変数選択は終了となります。変数選択には以下のような方法があります。
- 減少法:説明変数をすべて含むモデルからスタートし、1つずつ変数を減少させていく方法
- 増加法:説明変数を含まないモデルからスタートし、1つずつ変数を増加させていく方法
- 減増法:説明変数をすべて含むモデルからスタートし、1つずつ変数を増加させたり減少させたりする方法
- 増減法:説明変数を含まないモデルからスタートし、1つずつ変数を増加させたり減少させたりする方法
変数選択を行うための基準に「AIC」と「BIC」があります。AICは「赤池情報量規準」とよばれるもので、値が小さいほどあてはまりが良いモデルであると考えることができます。AICは次の式から計算することができます。
![]() はモデルの対数尤度を、
はモデルの対数尤度を、![]() は説明変数の数を表します。一方のBICは「ベイズ情報量規準」とよばれるもので、AICと同様、値が小さいほどあてはまりが良いモデルであると考えることができます。BICは次の式から計算することができます。
は説明変数の数を表します。一方のBICは「ベイズ情報量規準」とよばれるもので、AICと同様、値が小さいほどあてはまりが良いモデルであると考えることができます。BICは次の式から計算することができます。
![]() はモデルの対数尤度を、
はモデルの対数尤度を、![]() は説明変数の数を、
は説明変数の数を、![]() はサンプルサイズを表します。AICとBICはどちらを使うべきであるといった決まりはありません。ただし両者は計算式が異なるため、AICによって選択されたモデルとBICによって選択されたモデルが異なる場合があります。
はサンプルサイズを表します。AICとBICはどちらを使うべきであるといった決まりはありません。ただし両者は計算式が異なるため、AICによって選択されたモデルとBICによって選択されたモデルが異なる場合があります。
8. 多変量解析
- 8-1. ロジスティック回帰分析1
- 8-2. ロジスティック回帰分析2
- 8-3. ロジスティック回帰分析3
- 8-4. 階層型クラスター分析1
- 8-5. 階層型クラスター分析2
- 8-6. 非階層型クラスター分析







