- Step2. 中級編
- 8. 多変量解析
8-6. 非階層型クラスター分析
次に、非階層型(的)クラスター分析の1つであるk-means法について説明します。k-means法はサンプルサイズの大きな標本を分類するときに適した方法です。
■解析の流れ
次のようなデータを考えます。k-means法を使ってこのデータを3つのクラスターに分けてみます。

- データをランダムに分類する
- クラスターごとに重心を計算する
- 各データを最も距離が近い重心のクラスターに分類し直す
- 再度、クラスターごとに重心を計算する
- 再度、各データを最も距離が近い重心のクラスターに分類し直す
- 重心の計算と、各クラスターへの分類を繰り返す
各データを3つのクラスター(赤、青、緑)にランダムに分類します。
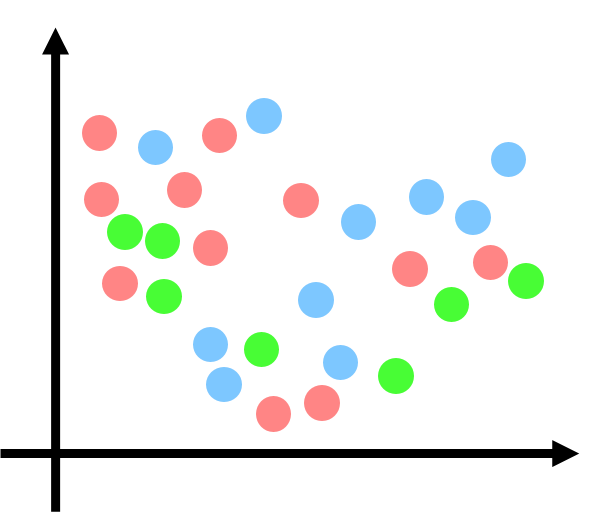
各クラスターに属するデータを使って重心(濃い赤、濃い青、濃い緑)を計算します。
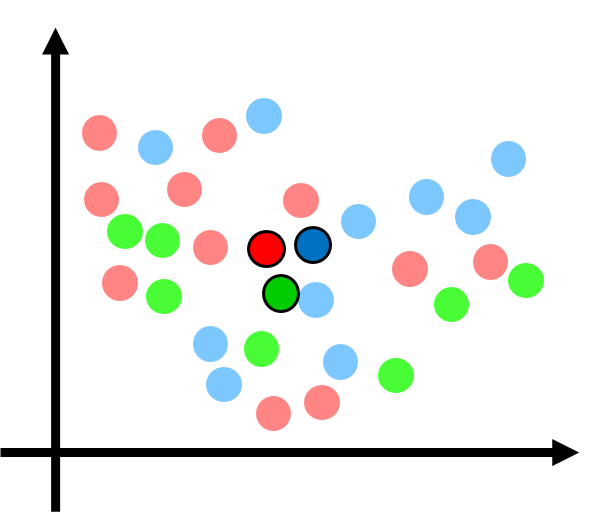
ランダムにクラスターに分類されたデータを、重心までの距離が最も近いクラスターに分類し直します(=所属するクラスターを変更します)。

各クラスターに属するデータを使って重心(濃い赤、濃い青、濃い緑)を計算します。

ランダムにクラスターに分類されたデータを、重心までの距離が最も近いクラスターに分類し直します(=所属するクラスターを変更します)。

「新しいクラスターに分類し直したデータを使った重心の計算」と「重心に基づく各クラスターへのデータ再分類」を繰り返し、データの動きがなくなったら計算終了です。

■損失関数
k-means法では、![]() 個のデータ
個のデータ ![]() に対して、次の式で表される損失関数
に対して、次の式で表される損失関数 ![]() を最小にするようにクラスタリングが行われます。
を最小にするようにクラスタリングが行われます。
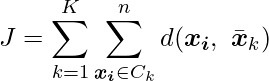
ここで、![]() はクラスター数を、
はクラスター数を、![]() は
は ![]() 番目のクラスターを表します。また、
番目のクラスターを表します。また、![]() は各クラスターに所属するデータとそのクラスターの重心との距離を表します。
は各クラスターに所属するデータとそのクラスターの重心との距離を表します。
最終的には、![]() の動きがなくなるまで計算を繰り返します。このときの値を
の動きがなくなるまで計算を繰り返します。このときの値を ![]() とすると、最も重心までの距離が近いクラスターへの再分類は次の式で表すことができます。
とすると、最も重心までの距離が近いクラスターへの再分類は次の式で表すことができます。
■k-means法の使い方
- k-means法は階層型クラスター分析よりも計算量が少なく、サンプルサイズが比較的大きなデータを分類するのに適している
<メリット>
<デメリット>
8. 多変量解析
- 8-1. ロジスティック回帰分析1
- 8-2. ロジスティック回帰分析2
- 8-3. ロジスティック回帰分析3
- 8-4. 階層型クラスター分析1
- 8-5. 階層型クラスター分析2
- 8-6. 非階層型クラスター分析







