- Step2. 中級編
- 8. 多変量解析
8-4. 階層型クラスター分析1
クラスター分析は、データの持つ様々な特徴をもとにサンプルどうしの類似度(距離)を計算し、データをいくつかのグループに分類する方法です。データをグループに分けることをクラスタリングといいます。クラスター分析には複数の手法があり、大きく階層型(的)クラスター分析と非階層型(的)クラスター分析に分けることができます。ここではまず、階層型クラスター分析について説明します。
例題:
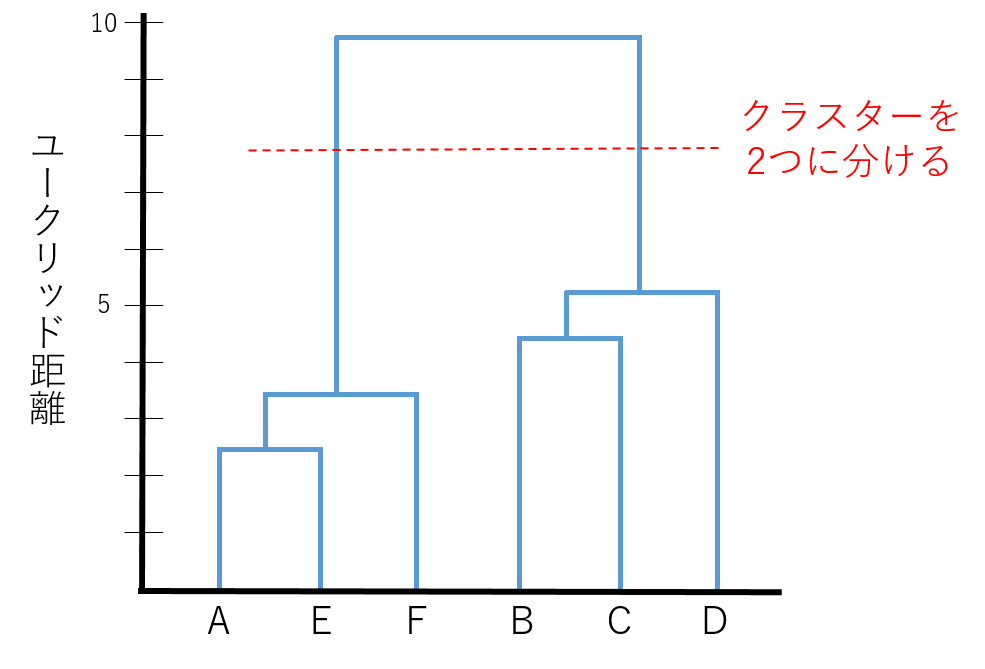
次のデータは、あるクラスの6人の生徒におけるテストの点数(10点満点)をまとめたものです。このデータを使って階層型クラスター分析を行い、生徒を2つのクラスターに分けてください。
| 生徒 | 国語 | 数学 | 理科 | 社会 | 英語 |
|---|---|---|---|---|---|
| A | 3 | 10 | 9 | 4 | 9 |
| B | 7 | 4 | 4 | 8 | 10 |
| C | 10 | 6 | 5 | 10 | 10 |
| D | 9 | 5 | 2 | 7 | 6 |
| E | 2 | 10 | 10 | 4 | 7 |
| F | 5 | 8 | 9 | 3 | 8 |
階層型クラスター分析ではまず、得られたデータからサンプル間の距離や相関係数を計算し、サンプル間の類似度を計算します。次の結果は、統計ソフトRを使ってサンプル間の「ユークリッド距離」を算出したものになります。値が小さいほど距離が近い=類似度が高いことを表します。

次に、類似度が最も高いものから順にクラスターに結合していきます。上で示した距離行列から最も距離が近いのは「AとE」です。したがって、「A」と「E」を結合します。
結合した後の距離計算には「重心法」を使います。すなわち、「A」と「E」の重心を、結合後の値とし、再度サンプル間のユークリッド距離を計算します。
| 生徒 | 国語 | 数学 | 理科 | 社会 | 英語 |
|---|---|---|---|---|---|
| AE | 2.5 | 10 | 9.5 | 4 | 8 |
| B | 7 | 4 | 4 | 8 | 10 |
| C | 10 | 6 | 5 | 10 | 10 |
| D | 9 | 5 | 2 | 7 | 6 |
| F | 5 | 8 | 9 | 3 | 8 |

上で示した距離行列から最も距離が近いのは「AEとF」です。したがって、「AE」と「F」を結合し、再度ユークリッド距離を計算します。
| 生徒 | 国語 | 数学 | 理科 | 社会 | 英語 |
|---|---|---|---|---|---|
| AEF | 3.75 | 9 | 9.25 | 3.5 | 8 |
| B | 7 | 4 | 4 | 8 | 10 |
| C | 10 | 6 | 5 | 10 | 10 |
| D | 9 | 5 | 2 | 7 | 6 |
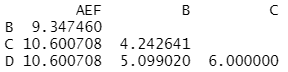
上で示した距離行列から最も距離が近いのは「BとC」です。したがって、「B」と「C」を結合し、再度ユークリッド距離を計算します。
| 生徒 | 国語 | 数学 | 理科 | 社会 | 英語 |
|---|---|---|---|---|---|
| AEF | 3.75 | 9 | 9.25 | 3.5 | 8 |
| BC | 8.5 | 5 | 4.5 | 9 | 10 |
| D | 9 | 5 | 2 | 7 | 6 |

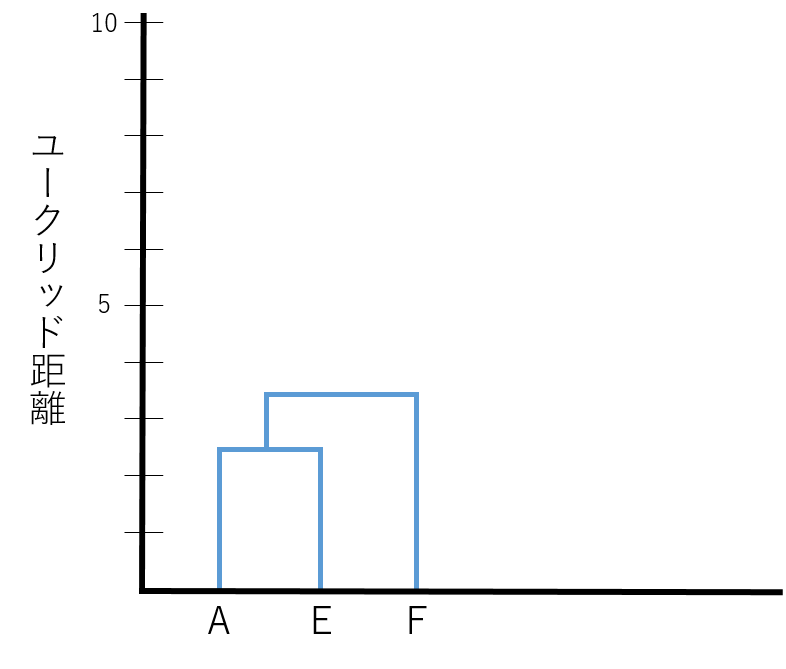
上で示した距離行列から最も距離が近いのは「BCとD」です。したがって、「BC」と「D」を結合し、再度ユークリッド距離を計算します。
| 生徒 | 国語 | 数学 | 理科 | 社会 | 英語 |
|---|---|---|---|---|---|
| AEF | 3.75 | 9 | 9.25 | 3.5 | 8 |
| BCD | 8.75 | 5 | 3.25 | 8 | 8 |
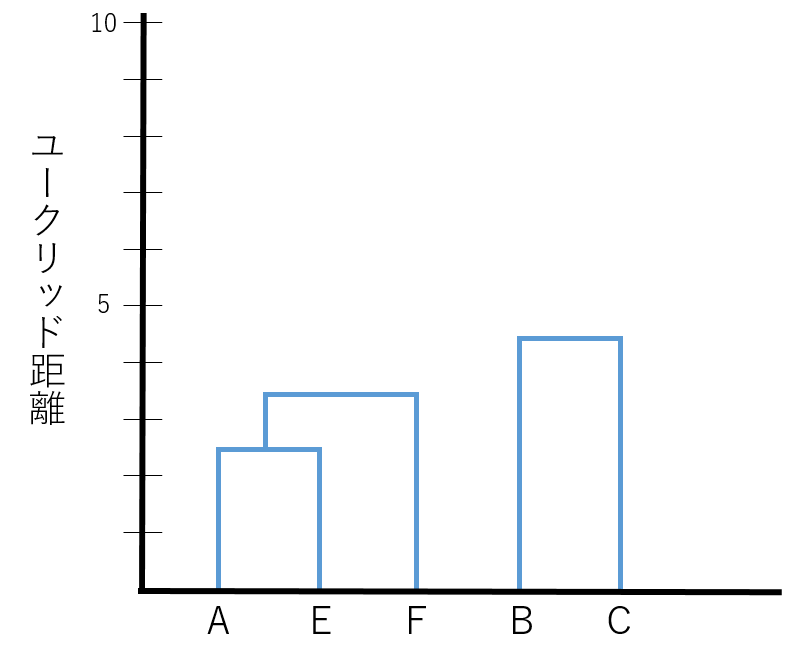
ここまでで、クラスター分析における類似度の計算は終わりです。ここまでの結果をまとめると、
- AとEを結合(距離:2.449490)
- AEとFを結合(距離:3.391165)
- BとCを結合(距離:4.242641)
- BCとDを結合(距離:5.147815)
- AEFとBCDを結合(距離:9.861541)
となり、最終的に1つのクラスターとなります。
■デンドログラム
クラスター分析において、このような結合の過程をグラフに表したものがデンドログラム(樹形図)です。デンドログラムを見ると、逐次的にサンプルがクラスタリングされる様子が分かります。
- AとEを結合(距離:2.449490)
- AEとFを結合(距離:3.391165)
- BとCを結合(距離:4.242641)
- BCとDを結合(距離:5.147815)
- AEFとBCDを結合(距離:9.861541)

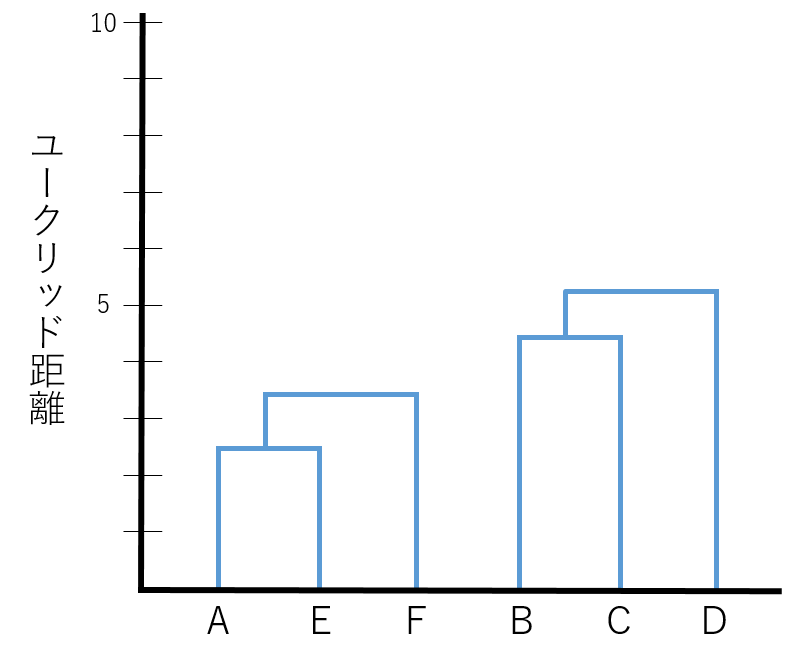
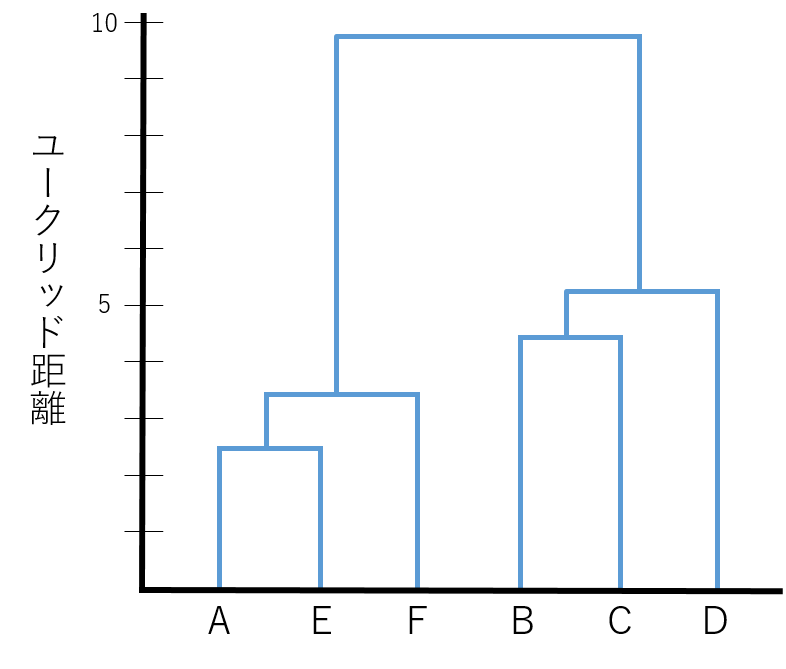
クラスター分析によって最終的に得られるのがこのデンドログラムです。この結果から、「A、E、F」と「B、C、D」の2つのクラスターに分けられることが分かります。
8. 多変量解析
- 8-1. ロジスティック回帰分析1
- 8-2. ロジスティック回帰分析2
- 8-3. ロジスティック回帰分析3
- 8-4. 階層型クラスター分析1
- 8-5. 階層型クラスター分析2
- 8-6. 非階層型クラスター分析







