- Step2. 中級編
- 8. 多変量解析
8-2. ロジスティック回帰分析2
例題:
次のデータは、あるお店に来た客30人について飲料Aを購入したかどうかを集計した結果です。「購入有無」に加え、調査日の「気温」、購入者の「性別」、購入した「時間帯」についても調べました。このデータから、飲料Aの購入確率を予測するロジスティックモデルを作成してください。
| No | 購入有無 | 性別 | 気温(℃) | 購入時間 |
|---|---|---|---|---|
| 1 | 購入した | 女性 | 16 | 午前中 |
| 2 | 購入した | 女性 | 22 | 午前中 |
| 3 | 購入した | 男性 | 21 | 午前中 |
| 4 | 購入した | 女性 | 16 | 午前中 |
| 5 | 購入した | 女性 | 19 | 午前中 |
| 6 | 購入した | 女性 | 15 | 午前中 |
| 7 | 購入した | 男性 | 20 | 午後 |
| 8 | 購入した | 女性 | 15 | 午前中 |
| 9 | 購入した | 女性 | 21 | 午後 |
| 10 | 購入した | 女性 | 17 | 午前中 |
| 11 | 購入した | 女性 | 19 | 午前中 |
| 12 | 購入した | 女性 | 20 | 午後 |
| 13 | 購入した | 男性 | 22 | 午前中 |
| 14 | 購入した | 女性 | 18 | 午後 |
| 15 | 購入した | 男性 | 22 | 午前中 |
| 16 | 購入した | 女性 | 23 | 午前中 |
| 17 | 購入した | 男性 | 18 | 午前中 |
| 18 | 購入した | 女性 | 20 | 午後 |
| 19 | 購入しなかった | 男性 | 22 | 午前中 |
| 20 | 購入しなかった | 男性 | 20 | 午後 |
| 21 | 購入しなかった | 男性 | 19 | 午後 |
| 22 | 購入しなかった | 男性 | 21 | 午前中 |
| 23 | 購入しなかった | 男性 | 22 | 午前中 |
| 24 | 購入しなかった | 女性 | 18 | 午後 |
| 25 | 購入しなかった | 男性 | 22 | 午後 |
| 26 | 購入しなかった | 男性 | 23 | 午後 |
| 27 | 購入しなかった | 男性 | 18 | 午後 |
| 28 | 購入しなかった | 女性 | 20 | 午後 |
| 29 | 購入しなかった | 男性 | 22 | 午前中 |
| 30 | 購入しなかった | 男性 | 20 | 午後 |
■データの前処理
テキストデータをすべて数値データにするため、元データを次のように変換します。
- 購入:「0」購入しなかった、「1」購入した
- 性別:「0」男性、「1」女性
- 購入時間:「0」午前中、「1」午後
変換したデータを次に示します。
| No | 購入有無 | 性別 | 気温(℃) | 購入時間 |
|---|---|---|---|---|
| 1 | 1 | 1 | 16 | 0 |
| 2 | 1 | 1 | 22 | 0 |
| 3 | 1 | 0 | 21 | 0 |
| 4 | 1 | 1 | 16 | 0 |
| 5 | 1 | 1 | 19 | 0 |
| 6 | 1 | 1 | 15 | 0 |
| 7 | 1 | 0 | 20 | 1 |
| 8 | 1 | 1 | 15 | 0 |
| 9 | 1 | 1 | 21 | 1 |
| 10 | 1 | 1 | 17 | 0 |
| 11 | 1 | 1 | 19 | 0 |
| 12 | 1 | 1 | 20 | 1 |
| 13 | 1 | 0 | 22 | 0 |
| 14 | 1 | 1 | 18 | 1 |
| 15 | 1 | 0 | 22 | 0 |
| 16 | 1 | 1 | 23 | 0 |
| 17 | 1 | 0 | 18 | 0 |
| 18 | 1 | 1 | 20 | 1 |
| 19 | 0 | 0 | 22 | 0 |
| 20 | 0 | 0 | 20 | 1 |
| 21 | 0 | 0 | 19 | 1 |
| 22 | 0 | 0 | 21 | 0 |
| 23 | 0 | 0 | 22 | 0 |
| 24 | 0 | 1 | 18 | 1 |
| 25 | 0 | 0 | 22 | 1 |
| 26 | 0 | 0 | 23 | 1 |
| 27 | 0 | 0 | 18 | 1 |
| 28 | 0 | 1 | 20 | 1 |
| 29 | 0 | 0 | 22 | 0 |
| 30 | 0 | 0 | 20 | 1 |
■Rによる解析結果
統計ソフトRを使ってロジスティック回帰分析を行うと、次のような結果が得られます。
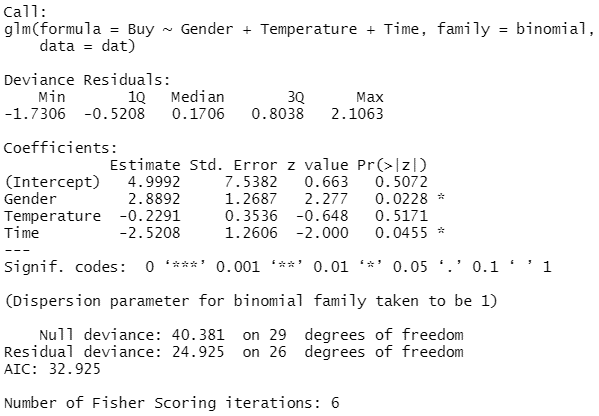
■偏回帰係数の推定値
「Coefficients」の「Estimate」が解析によって得られた偏回帰係数の推定値です。購入有無 ![]() を目的変数とし、性別(Gender)
を目的変数とし、性別(Gender)![]() 、気温(Temperature)
、気温(Temperature)![]() 、購入時間(Time)
、購入時間(Time)![]() を説明変数とすると、推定されたロジスティック回帰式を次のように書くことができます。
を説明変数とすると、推定されたロジスティック回帰式を次のように書くことができます。
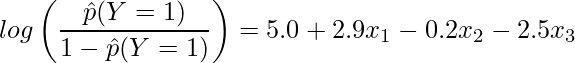
偏回帰係数が ![]() の場合は
の場合は ![]() のオッズ(あるいはロジット)を増加させるため
のオッズ(あるいはロジット)を増加させるため ![]() の発生確率を上昇させます。一方、偏回帰係数が
の発生確率を上昇させます。一方、偏回帰係数が ![]() の場合は
の場合は ![]() のオッズ(あるいはロジット)を減少させるため
のオッズ(あるいはロジット)を減少させるため ![]() の発生確率を低下させます。
の発生確率を低下させます。
ロジスティック回帰分析の結果から次のようなことが分かります。
- 性別(Gender)の偏回帰係数(
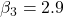 )の検定結果はP値=0.0228となっており、性別=1(女性)では性別=0(男性)と比べて購入確率が有意に上昇することが予想されます。
)の検定結果はP値=0.0228となっており、性別=1(女性)では性別=0(男性)と比べて購入確率が有意に上昇することが予想されます。 - 購入時間(Time)の偏回帰係数(
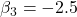 )の検定結果はP値=0.0455となっており、購入時間=0(午前中)では購入時間=1(午後)と比べて購入確率が有意に上昇することが予想されます。
)の検定結果はP値=0.0455となっており、購入時間=0(午前中)では購入時間=1(午後)と比べて購入確率が有意に上昇することが予想されます。 - 気温(Temperature)の偏回帰係数(
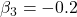 )の検定結果はP値=0.5171となっており、購入確率に有意な影響を与えないと予想されます。
)の検定結果はP値=0.5171となっており、購入確率に有意な影響を与えないと予想されます。
■偏回帰係数の有意性の検定
偏回帰係数の有意性の検定とは、定数項も含めた各偏回帰係数が0であるかについての検定結果です。帰無仮説は「偏回帰係数=0」です。偏回帰係数の推定値 ![]() をその標準誤差
をその標準誤差 ![]() で割って2乗した値(
で割って2乗した値(![]() )について、自由度1のカイ二乗分布を用いて検定を行います。このような検定をWald検定といいます。
)について、自由度1のカイ二乗分布を用いて検定を行います。このような検定をWald検定といいます。
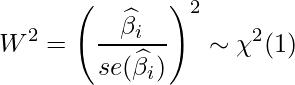
この検定により有意となった場合、偏回帰係数は0ではない、すなわちその説明変数の目的変数に対する影響は統計的に有意であると言うことができます。
例えば、性別(Gender)の偏回帰係数の有意性の検定では ![]() 値は次のように算出されます。ちなみに、「Coefficients」の「Std. Error」が解析によって得られた偏回帰係数の推定値の標準誤差です。
値は次のように算出されます。ちなみに、「Coefficients」の「Std. Error」が解析によって得られた偏回帰係数の推定値の標準誤差です。
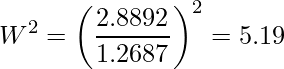
カイ二乗分布表から、![]() の値は「3.84」であることから、「有意水準5%において、帰無仮説は棄却され対立仮説が採択される」という結果になります。つまり、「性別(Gender)の偏回帰係数は購入確率に有意な影響を与えている」と結論づけられます。
の値は「3.84」であることから、「有意水準5%において、帰無仮説は棄却され対立仮説が採択される」という結果になります。つまり、「性別(Gender)の偏回帰係数は購入確率に有意な影響を与えている」と結論づけられます。
■偏回帰係数の信頼区間
次の式から偏回帰係数の95%信頼区間を求めることができます。
例えば、性別(Gender)の偏回帰係数の95%信頼区間は次のように算出されます。
このように、95%信頼区間が0をまたいでいない場合には、その偏回帰係数は有意であると判断できます。
■偏回帰係数の解釈
目的変数が0/1からなる2値データ ![]() が
が ![]() となる確率を
となる確率を ![]() 、
、![]() 個の説明変数
個の説明変数 ![]() をそれぞれ
をそれぞれ ![]() 、偏回帰係数をそれぞれ
、偏回帰係数をそれぞれ ![]() とすると、ロジスティック回帰モデルは次の式で表すことができます。
とすると、ロジスティック回帰モデルは次の式で表すことができます。
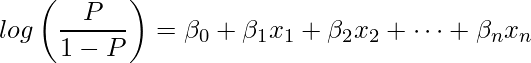
![]() が1単位増加した場合に
が1単位増加した場合に ![]() となる確率を
となる確率を ![]() とすると、ロジスティック回帰モデルは次のようになります。
とすると、ロジスティック回帰モデルは次のようになります。
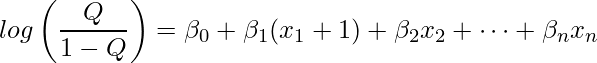
下の式から上の式を引くと、
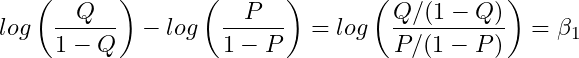
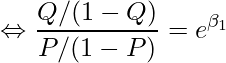
となります。 すなわち、![]() に対して自然対数を底とする指数変換を行うと、「
に対して自然対数を底とする指数変換を行うと、「![]() を1単位増加させる前」に対する「
を1単位増加させる前」に対する「![]() を1単位増加させた後」のオッズ比を算出することができます。このオッズ比が1を超える場合、
を1単位増加させた後」のオッズ比を算出することができます。このオッズ比が1を超える場合、![]() のオッズを高めます。
のオッズを高めます。
例えば、性別(Gender)が1増加した場合(男性に対する女性)のオッズ比は次のように計算できます。
この結果より、飲料Aの購入確率のオッズは18.2倍となり、男性に比べて女性の方が購入確率が高くなると予想されます。
また、次の式からオッズ比 ![]() の95%信頼区間を求めることができます。
の95%信頼区間を求めることができます。![]() は標準誤差を表します。
は標準誤差を表します。
例えば、性別(Gender)のオッズ比の95%信頼区間は次のように算出されます。
このように、95%信頼区間が1をまたいでいない場合には、そのオッズ比は有意であると判断できます。
8. 多変量解析
- 8-1. ロジスティック回帰分析1
- 8-2. ロジスティック回帰分析2
- 8-3. ロジスティック回帰分析3
- 8-4. 階層型クラスター分析1
- 8-5. 階層型クラスター分析2
- 8-6. 非階層型クラスター分析






