- Step2. 中級編
- 6. ノンパラメトリック検定
6-5. ノンパラメトリック検定 – 対応のない3群以上のデータの差の検定
29章では3群以上からなるデータの平均値の差の検定方法である分散分析について学びました。
ここでは、一元配置分散分析のノンパラメトリック検定版である「クラスカル=ウォリス検定」について学びます。
■クラスカル=ウォリス検定
![]() 群からなるデータをひとまとめにして順位をつけます。タイデータに対しては、順位の中央値を使用します。付与した順位を群ごとに足し合わせ、順位の合計値
群からなるデータをひとまとめにして順位をつけます。タイデータに対しては、順位の中央値を使用します。付与した順位を群ごとに足し合わせ、順位の合計値 ![]() を算出します。
を算出します。![]() と各群のサンプルサイズ
と各群のサンプルサイズ ![]() を用いて次の式からクラスカル=ウォリスの統計量
を用いて次の式からクラスカル=ウォリスの統計量 ![]() を計算します(
を計算します(![]() は全データの総数を表します)。この
は全データの総数を表します)。この ![]() が近似的に自由度
が近似的に自由度 ![]() のカイ二乗分布に従うことを用いて検定を行います。
のカイ二乗分布に従うことを用いて検定を行います。
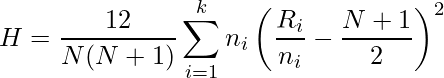
あるいは
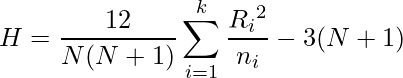
次のデータを使ってクラスカル=ウォリス検定を行ってみます。
| No. | A班の身長(cm) | B班の身長(cm) | C班の身長(cm) |
|---|---|---|---|
| 1 | 170 | 155 | 170 |
| 2 | 155 | 165 | 145 |
| 3 | 140 | 180 | 150 |
| 4 | 165 | 185 | 135 |
| 5 | 160 | 175 | - |
| 6 | - | 160 | - |
- 全体の値に対して順位を付与
- 標本ごとに順位の和を算出
- クラスカル=ウォリス検定を行う
身長を小さい順に並べると「135 < 140 < 145 < 150 < 155, 155 < 160, 160 < 165, 165 < 170, 170 < 175 < 180 < 185」となります。
並べ替えた身長に対して順位を付与すると「1 < 2 < 3 < 4 < 5.5, 5.5 < 7.5, 7.5 < 9.5, 9.5 < 11.5, 11.5 < 13 < 114 < 15」となります。
| No. | A班の身長(cm) | B班の身長(cm) | C班の身長(cm) |
|---|---|---|---|
| 1 | 11.5 | 5.5 | 11.5 |
| 2 | 5.5 | 9.5 | 3 |
| 3 | 2 | 14 | 4 |
| 4 | 9.5 | 15 | 1 |
| 5 | 7.5 | 13 | - |
| 6 | - | 7.5 | - |
| No. | A班の身長(cm) | B班の身長(cm) | C班の身長(cm) |
|---|---|---|---|
| 1 | 11.5 | 5.5 | 11.5 |
| 2 | 5.5 | 9.5 | 3 |
| 3 | 2 | 14 | 4 |
| 4 | 9.5 | 15 | 1 |
| 5 | 7.5 | 13 | - |
| 6 | - | 7.5 | - |
| R(順位和) | 36 | 64.5 | 19.5 |
| n(サンプルサイズ) | 5 | 6 | 4 |
検定統計量 ![]() を計算すると
を計算すると
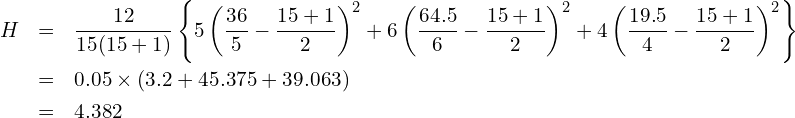
となります。自由度 ![]() のカイ二乗検定を用いて検定を行うと、
のカイ二乗検定を用いて検定を行うと、![]() となる確率(片側検定のP値)を求めると
となる確率(片側検定のP値)を求めると ![]() となります。クラスカル=ウォリス検定では、平均順位に対する各変数における順位のズレがどのくらい大きかについて検定をするので、必ず「片側検定」となります。
となります。クラスカル=ウォリス検定では、平均順位に対する各変数における順位のズレがどのくらい大きかについて検定をするので、必ず「片側検定」となります。
6. ノンパラメトリック検定
- 6-1. ノンパラメトリック検定とは
- 6-2. ノンパラメトリック検定 – 順位相関係数
- 6-3. ノンパラメトリック検定 – 対応のない2標本の差の検定
- 6-4. ノンパラメトリック検定 – 対応のある2標本の差の検定
- 6-5. ノンパラメトリック検定 – 対応のない3群以上のデータの差の検定







