- Step2. 中級編
- 6. ノンパラメトリック検定
6-2. ノンパラメトリック検定 – 順位相関係数
26-3章で学んだピアソンの積率相関係数はデータが正規分布をしている場合にのみ使うことができます。データが正規分布に従わない場合は、ノンパラメトリックな手法であるスピアマンの順位相関係数もしくはケンドールの順位相関係数を使います。これらはどちらを使っても良く、手法の選択に関するルールはありません。
■スピアマンの順位相関係数
各変数の値を順位に変換してピアソンの積率相関係数を求めたものです。対になった変数![]() と
と![]() に
に![]() 対のデータがあるとき、
対のデータがあるとき、![]() と
と![]() のそれぞれの値に対して順位をつけます。
のそれぞれの値に対して順位をつけます。![]() 対すべてについて
対すべてについて![]() 番目のデータ
番目のデータ![]() と
と![]() の順位の差
の順位の差![]() を求めます。この
を求めます。この![]() を使って以下の式から順位相関係数
を使って以下の式から順位相関係数![]() を算出します。
を算出します。
2変数![]() と
と![]() のデータの順位が全て一致する場合は
のデータの順位が全て一致する場合は![]() 、どちらかの変数を逆順にする順位が全て一致する場合は
、どちらかの変数を逆順にする順位が全て一致する場合は![]() となります。
となります。
【タイ(同順位)データが無い場合】
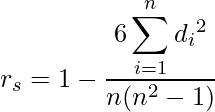
【タイデータがある場合】
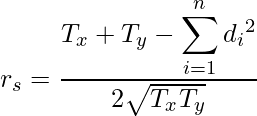
ただし、![]() と
と![]() は次の式から求めます。
は次の式から求めます。![]() と
と![]() はそれぞれ変数
はそれぞれ変数![]() と
と![]() におけるタイデータの個数を、
におけるタイデータの個数を、![]() と
と![]() は各タイデータ含まれるデータの数を表します。タイデータに対しては、順位の中央値を使用します。
は各タイデータ含まれるデータの数を表します。タイデータに対しては、順位の中央値を使用します。
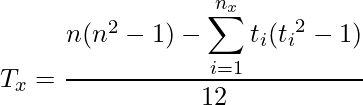
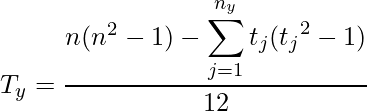
まず、タイデータを含まないデータからスピアマンの順位相関係数を求めてみます。
| 国語の点数 | 数学の点数 | |
|---|---|---|
| A | 100 | 90 |
| B | 95 | 80 |
| C | 85 | 100 |
| D | 80 | 75 |
| E | 70 | 50 |
| F | 60 | 60 |
- 各変数の順位を算出
- 順位の差を算出
- スピアマンの順位相関係数を算出
| 国語の点数の順位 | 数学の点数の順位 | |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 3 |
| C | 3 | 1 |
| D | 4 | 4 |
| E | 5 | 6 |
| F | 6 | 5 |
| 国語の点数の順位 | 数学の点数の順位 | 順位の差 | |
|---|---|---|---|
| A | 1 | 2 | -1 |
| B | 2 | 3 | -1 |
| C | 3 | 1 | 2 |
| D | 4 | 4 | 0 |
| E | 5 | 6 | -1 |
| F | 6 | 5 | 1 |
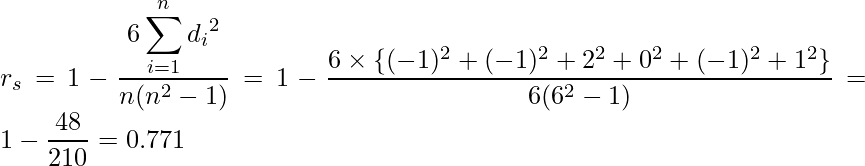
次に、タイデータを含むデータからスピアマンの順位相関係数を求めてみます。
| 国語の点数 | 数学の点数 | |
|---|---|---|
| A | 100 | 100 |
| B | 95 | 100 |
| C | 85 | 100 |
| D | 80 | 75 |
| E | 80 | 50 |
| F | 60 | 60 |
- 各変数の順位を算出
- 順位の差を算出
- スピアマンの順位相関係数を算出
タイデータには順位の中央値を付与します。
| 国語の点数の順位 | 数学の点数の順位 | |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 2 |
| C | 3 | 2 |
| D | 4.5 | 4 |
| E | 4.5 | 6 |
| F | 6 | 5 |
| 国語の点数の順位 | 数学の点数の順位 | 順位の差 | |
|---|---|---|---|
| A | 1 | 2 | -1 |
| B | 2 | 2 | 0 |
| C | 3 | 2 | 1 |
| D | 4.5 | 4 | 0.5 |
| E | 4.5 | 6 | -1.5 |
| F | 6 | 5 | 1 |
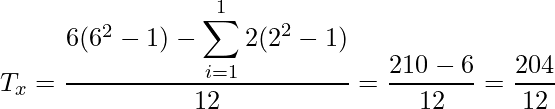
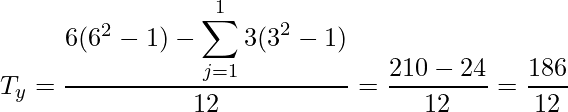
算出した![]() と
と![]() の値を用います。
の値を用います。
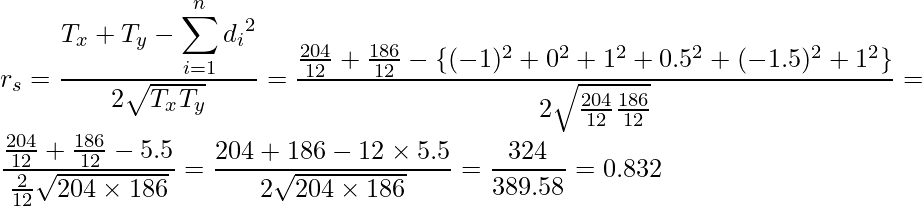
■ケンドールの順位相関係数
データのペアの順序関係が2つのリストにおいてどれだけ一致しているかを算出したものです。対応する2つの変量![]() (ただし、
(ただし、![]() )があるとき、その中から取り出した
)があるとき、その中から取り出した![]() と
と![]() (ただし、
(ただし、![]() )において、
)において、![]() と
と![]() の大小関係が同じかどうかを用いて順位相関係数を計算します。
の大小関係が同じかどうかを用いて順位相関係数を計算します。
2変数のデータの大小関係が全て一致する場合は![]() 、どちらかの変数を逆順にする大小関係が全て一致する場合は
、どちらかの変数を逆順にする大小関係が全て一致する場合は![]() となります。
となります。
【タイデータが無い場合】
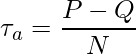
ただし、
- P =
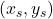 と
と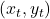 との大小関係が同じ向きである組の数 =
との大小関係が同じ向きである組の数 = 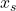 と
と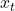 、
、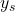 と
と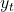 の大小関係が一致する組の数
の大小関係が一致する組の数 - Q =
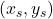 と
と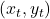 との大小関係が異なる向きである組の数 =
との大小関係が異なる向きである組の数 = 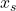 と
と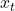 、
、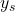 と
と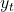 の大小関係が不一致である組の数
の大小関係が不一致である組の数 - N = 比較したデータの組の総数:
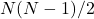
【タイデータがある場合】
タイデータに対しては、順位の中央値を使用します。
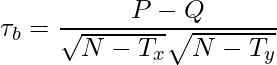
ただし、
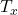 = (
= (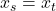 )である組の数
)である組の数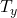 = (
= (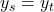 )である組の数
)である組の数
まず、タイデータを含まないデータからケンドールの順位相関係数を求めてみます。
| 国語の点数 | 数学の点数 | |
|---|---|---|
| A | 100 | 90 |
| B | 95 | 80 |
| C | 85 | 100 |
| D | 80 | 75 |
| E | 70 | 50 |
| F | 60 | 60 |
- 各変数の順位を算出
- すべてのペアの大小関係を調べる
- (1, 2)と(2, 3) → 一致
- (1, 2)と(3, 1) → 不一致
- (1, 2)と(4, 4) → 一致
- (1, 2)と(5, 6) → 一致
- (1, 2)と(6, 5) → 一致
- (2, 3)と(3, 1) → 不一致
- (2, 3)と(4, 4) → 一致
- (2, 3)と(5, 6) → 一致
- (2, 3)と(6, 5) → 一致
- (3, 1)と(4, 4) → 一致
- (3, 1)と(5, 6) → 不一致
- (3, 1)と(6, 5) → 一致
- (4, 4)と(5, 6) → 一致
- (4, 4)と(6, 5) → 一致
- (5, 6)と(6, 5) → 一致
- すべてのペアの大小関係を集計
- P = 12
- Q = 3
- N = 15
- ケンドールの順位相関係数を算出
| 国語の点数の順位 | 数学の点数の順位 | |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 3 |
| C | 3 | 1 |
| D | 4 | 4 |
| E | 5 | 6 |
| F | 6 | 5 |
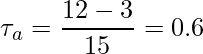
次に、タイデータを含むデータからスピアマンの順位相関係数を求めてみます。
| 国語の点数 | 数学の点数 | |
|---|---|---|
| A | 100 | 100 |
| B | 95 | 100 |
| C | 85 | 100 |
| D | 80 | 75 |
| E | 80 | 50 |
| F | 60 | 60 |
- 各変数の順位を算出
- すべてのペアの大小関係を調べる
- (1, 2)と(2, 2) → yが等しい
- (1, 2)と(3, 2) → yが等しい
- (1, 2)と(4, 4) → 一致
- (1, 2)と(5, 6) → 一致
- (1, 2)と(6, 5) → 一致
- (2, 2)と(3, 2) → yが等しい
- (2, 2)と(4.5, 4) → 一致
- (2, 2)と(4.5, 6) → 一致
- (2, 2)と(6, 5) → 一致
- (3, 2)と(4.5, 4) → 一致
- (3, 2)と(4.5, 6)→ 不一致
- (3, 2)と(6, 5) → 一致
- (4.5, 4)と(4.5, 6)→ xが等しい
- (4.5, 4)と(6, 5) → 一致
- (4.5, 6)と(6, 5) → 一致
- すべてのペアの大小関係を集計
- P = 10
- Q = 1
- N = 15
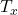 = 1
= 1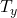 = 3
= 3- ケンドールの順位相関係数を算出
タイデータには順位の中央値を付与します。
| 国語の点数の順位 | 数学の点数の順位 | |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 2 |
| C | 3 | 2 |
| D | 4.5 | 4 |
| E | 4.5 | 6 |
| F | 6 | 5 |
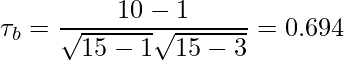
6. ノンパラメトリック検定
- 6-1. ノンパラメトリック検定とは
- 6-2. ノンパラメトリック検定 – 順位相関係数
- 6-3. ノンパラメトリック検定 – 対応のない2標本の差の検定
- 6-4. ノンパラメトリック検定 – 対応のある2標本の差の検定
- 6-5. ノンパラメトリック検定 – 対応のない3群以上のデータの差の検定







