- Step2. 中級編
- 6. ノンパラメトリック検定
6-4. ノンパラメトリック検定 – 対応のある2標本の差の検定
24-5章では対応のある2標本t検定について学びました。
ここでは、対応のある2標本t検定のノンパラメトリック検定版である「ウィルコクソンの符号付き順位検定」と「符号検定」について学びます。ちなみに「ウィルコクソンの符号付き順位検定」は3-4章で紹介した「ウィルコクソンの順位和検定」とは異なりますのでご注意ください。
■ウィルコクソンの符号付き順位検定
対応のある![]() 対のデータ
対のデータ ![]() のすべての対について、データの差
のすべての対について、データの差 ![]() を求めます。
を求めます。![]() となるものを除いて(サンプルサイズ
となるものを除いて(サンプルサイズ![]() も減らします)、絶対値
も減らします)、絶対値 ![]() が小さいものから順に並べて符号付きの順位を付けます。タイデータに対しては、順位の中央値を使用します。これらの順位を用いて、
が小さいものから順に並べて符号付きの順位を付けます。タイデータに対しては、順位の中央値を使用します。これらの順位を用いて、![]() が正の値の合計順位
が正の値の合計順位 ![]() と負の値の合計順位
と負の値の合計順位 ![]() をそれぞれ計算します。2つの合計順位のうち小さい方を検定統計量
をそれぞれ計算します。2つの合計順位のうち小さい方を検定統計量 ![]() とします。この場合、
とします。この場合、![]() が観測値以下の値を取る確率がP値となります。
が観測値以下の値を取る確率がP値となります。
また、サンプルサイズが大きい場合、次の式により得られた![]() と
と![]() から算出された
から算出された![]() が正規分布に従うことを利用して検定を行います。
が正規分布に従うことを利用して検定を行います。
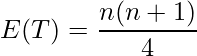
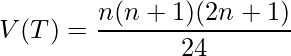
まず、サンプルサイズが小さいデータを使ってウィルコクソンの符号付き順位検定を行ってみます。
| No. | 特訓前50m走タイム(s) | 特訓後50m走タイム(s) |
|---|---|---|
| 1 | 10.0 | 9.0 |
| 2 | 8.5 | 8.0 |
| 3 | 7.0 | 9.0 |
| 4 | 9.5 | 7.0 |
| 5 | 6.5 | 6.5 |
| 6 | 7.5 | 7.0 |
- データの差を求める
- 符号付き順位を付与する(差=0となるデータは除外)
- 正の値の合計順位と負の値の合計順位を算出
- P値を算出し検定を行う
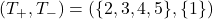
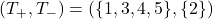
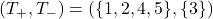
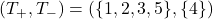
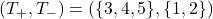
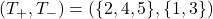
| No. | 特訓前50m走タイム(s) | 特訓後50m走タイム(s) | タイム差(特訓前-特訓後) |
|---|---|---|---|
| 1 | 10.0 | 9.0 | 1.0 |
| 2 | 8.5 | 8.0 | 1.5 |
| 3 | 7.0 | 9.0 | -2.0 |
| 4 | 9.5 | 7.0 | 2.5 |
| 5 | 6.5 | 6.5 | 0 |
| 6 | 7.5 | 7.0 | 0.5 |
| No. | 特訓前50m走タイム(s) | 特訓後50m走タイム(s) | タイム差(特訓前-特訓後) | 符号付き順位 |
|---|---|---|---|---|
| 1 | 10.0 | 9.0 | 1.0 | 2 |
| 2 | 8.5 | 8.0 | 1.5 | 3 |
| 3 | 7.0 | 9.0 | -2.0 | -4 |
| 4 | 9.5 | 7.0 | 2.5 | 5 |
| 6 | 7.5 | 7.0 | 0.5 | 1 |
検定統計量は ![]() となります。また、1から5までの順位が正もしくは負のいずれかに分けられるすべての組み合わせは
となります。また、1から5までの順位が正もしくは負のいずれかに分けられるすべての組み合わせは ![]() 通りです。このうち、
通りです。このうち、![]() となる組み合わせは、
となる組み合わせは、
の6通りです。したがって、求めるP値(片側検定)は
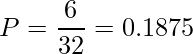
となります。また、両側検定のP値は![]() となります。すなわち特訓前後で50m走のタイムに有意差があるとは言えないと結論付けられます。
となります。すなわち特訓前後で50m走のタイムに有意差があるとは言えないと結論付けられます。
次に、サンプルサイズが大きいデータを使ってウィルコクソンの符号付き順位検定を行ってみます。
- データの差に対する符号順位から正の値の合計順位と負の値の合計順位を算出
- ウィルコクソンの順位和検定を行う
ここでは、![]() 、
、![]() とします。
とします。
E(T)とV(T)を求めます。
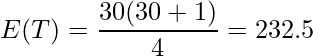
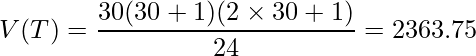
これらの値から算出したz値を用いて検定を行います。
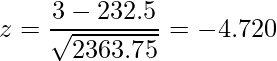
![]() (片側検定のP値)を求めると
(片側検定のP値)を求めると![]() となります。また、
となります。また、![]() (両側検定のP値)を求めると
(両側検定のP値)を求めると![]() となります。
となります。
ちなみに、実際のデータ(※ここではデータを示しません)から得た符号付き順位を元にP値を計算すると![]() となることから、正規近似により実際にP値にかなり近い値が得られていることが分かります。
となることから、正規近似により実際にP値にかなり近い値が得られていることが分かります。
■符号検定
対応のある![]() 対のデータ
対のデータ ![]() のすべての対について変数間の大小を比較し、「+(正:大きい)」「-(負:小さい)」「=(等しい)」の件数を調べ、「+」と「-」の数のうち小さい方を検定統計量
のすべての対について変数間の大小を比較し、「+(正:大きい)」「-(負:小さい)」「=(等しい)」の件数を調べ、「+」と「-」の数のうち小さい方を検定統計量 ![]() とします。変数間に差がない場合、全データ対のうち半数が「+」に、残りの半分が「-」になると予想されます。したがって、サンプルサイズが小さい場合には、各符号の出現率が
とします。変数間に差がない場合、全データ対のうち半数が「+」に、残りの半分が「-」になると予想されます。したがって、サンプルサイズが小さい場合には、各符号の出現率が ![]() の二項分布に従うことを利用して検定を行います。
の二項分布に従うことを利用して検定を行います。![]() が観測値以下の値を取る確率がP値となります。「=(等しい)」データ対は検定から除外します(サンプルサイズ
が観測値以下の値を取る確率がP値となります。「=(等しい)」データ対は検定から除外します(サンプルサイズ![]() も減らします)。
も減らします)。
また、サンプルサイズが大きい場合、次の式により得られた![]() と
と![]() から算出された
から算出された![]() が正規分布に従うことを利用して検定を行います。
が正規分布に従うことを利用して検定を行います。
まず、サンプルサイズが小さいデータを使って符号検定を行ってみます。
| No. | 特訓前50m走タイム(s) | 特訓後50m走タイム(s) |
|---|---|---|
| 1 | 10.0 | 9.0 |
| 2 | 8.0 | 8.5 |
| 3 | 7.0 | 9.0 |
| 4 | 9.5 | 7.0 |
| 5 | 6.5 | 6.5 |
| 6 | 7.5 | 7.0 |
- データの大小を比較
- 検定を行う
- データの差から「+(正:大きい)」「-(負:小さい)」「=(等しい)」の件数を集計する
- 符号検定を行う
| No. | 特訓前50m走タイム(s) | 特訓後50m走タイム(s) | データの大小(特訓前-特訓後) |
|---|---|---|---|
| 1 | 10.0 | 9.0 | + |
| 2 | 8.5 | 8.0 | + |
| 3 | 7.0 | 9.0 | - |
| 4 | 9.5 | 7.0 | + |
| 5 | 6.5 | 6.5 | = |
| 6 | 7.5 | 7.0 | + |
No.5のデータは「=(等しい)」ため、検定から除外します。
二項分布を用いて5回のベルヌーイ試行を行うときに「-」が1回以下となる確率、すなわち![]() となる確率(片側検定のP値)は次の式から計算することができます。
となる確率(片側検定のP値)は次の式から計算することができます。
また、両側検定の場合のP値は![]() となります。すなわち特訓前後で50m走のタイムに有意差があるとは言えないと結論付けられます。
となります。すなわち特訓前後で50m走のタイムに有意差があるとは言えないと結論付けられます。
次に、サンプルサイズが大きいデータを使って符号検定を行ってみます。
ここでは、「+」=22、「-」=10、「=」=2とします。
検定統計量は ![]() 、サンプルサイズは
、サンプルサイズは![]() となります(「=」のデータは除外します)。次の式からE(m)とV(m)を求めます。
となります(「=」のデータは除外します)。次の式からE(m)とV(m)を求めます。
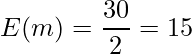
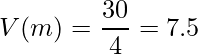
これらの値から算出したz値を用いて検定を行います。
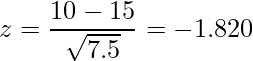
![]() (片側検定のP値)を求めると
(片側検定のP値)を求めると![]() となります。また、
となります。また、![]() (両側検定のP値)を求めると
(両側検定のP値)を求めると![]() となります。
となります。
6. ノンパラメトリック検定
- 6-1. ノンパラメトリック検定とは
- 6-2. ノンパラメトリック検定 – 順位相関係数
- 6-3. ノンパラメトリック検定 – 対応のない2標本の差の検定
- 6-4. ノンパラメトリック検定 – 対応のある2標本の差の検定
- 6-5. ノンパラメトリック検定 – 対応のない3群以上のデータの差の検定







