- Step2. 中級編
- 6. ノンパラメトリック検定
6-3. ノンパラメトリック検定 – 対応のない2標本の差の検定
24-4章で対応のない2標本t検定について学びました。t検定は2つの群の母集団の分散が等しく、ともに独立した正規分布に従うことを前提としています。
ここでは、対応のない2標本t検定のノンパラメトリック検定版である「ウィルコクソンの順位和検定」と「並べ替え検定」について学びます。
■ウィルコクソンの順位和検定
まず、比較する2標本の全体の値に対して順位をつけます。タイデータに対しては、順位の中央値を使用します。付与した順位を標本ごとに足し合わせ、順位の合計値を算出します。ここでは2つの標本を![]() と
と![]() とし、順位の合計値をそれぞれ
とし、順位の合計値をそれぞれ![]() と
と![]() 、サンプルサイズをそれぞれ
、サンプルサイズをそれぞれ![]() と
と![]() とします。2つの合計順位のうち小さい方を検定統計量
とします。2つの合計順位のうち小さい方を検定統計量 ![]() とします。順位の全ての組み合わせ
とします。順位の全ての組み合わせ ![]() のうち、
のうち、![]() が観測値以下の値を取る確率がP値となります。
が観測値以下の値を取る確率がP値となります。
また、サンプルサイズが大きい場合は、次の式より得られた ![]() と
と ![]() から算出された
から算出された ![]() が正規分布に従うことを利用して検定を行います。
が正規分布に従うことを利用して検定を行います。
【タイ(同順位)データが無い場合】
ここでは![]() とします。
とします。
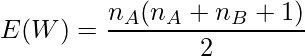
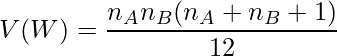
【タイデータがある場合】
![]() はタイデータの個数を、
はタイデータの個数を、![]() は各タイデータ含まれるデータの数を表します。
は各タイデータ含まれるデータの数を表します。
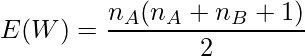
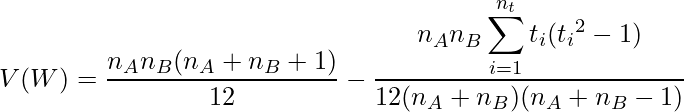
まず、サンプルサイズが小さいデータを使ってウィルコクソンの順位和検定を行ってみます。
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 26 | 30 |
| 2 | 32 | 35 |
| 3 | 25 | 36 |
| 4 | 20 | - |
- 全体の値に対して順位を付与
- 標本ごとに順位の和を算出
- ウィルコクソンの順位和検定を行う
- (A, B) = ({1, 2, 3, 4}, {5, 6, 7}) ※
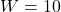
- (A, B) = ({1, 2, 3, 5}, {4, 6, 7}) ※
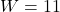
- 全体の値に対して順位を付与
- 標本ごとに順位の和を算出
- ウィルコクソンの順位和検定を行う
- 全体の値に対して順位を付与
- 標本ごとに順位の和を算出
- ウィルコクソンの順位和検定を行う
- すべてのデータを用いて2群に分ける全ての組み合わせを考える
- 20通りの組み合わせそれぞれの平均値の差を求める
- 観測された組み合わせ以上に差が大きくなる組み合わせを選ぶ
- 検定を行う
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 3 | 4 |
| 2 | 5 | 6 |
| 3 | 2 | 7 |
| 4 | 1 | - |
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 3 | 4 |
| 2 | 5 | 6 |
| 3 | 2 | 7 |
| 4 | 1 | - |
| 合計 | 11 | 17 |
この例題では ![]() であることから、
であることから、![]() となります。
となります。![]() となる組み合わせは
となる組み合わせは
の2通りです。順位の全ての組み合わせは ![]() なので、
なので、![]() となる確率(片側検定のP値)を求めると
となる確率(片側検定のP値)を求めると![]() となります。
となります。
両側検定のP値を求めると![]() となります。すなわち2群間で年齢の分布に有意差があるとは言えないと結論付けられます。
となります。すなわち2群間で年齢の分布に有意差があるとは言えないと結論付けられます。
次に、タイデータを含まないデータから算出した ![]() と
と ![]() を使ってウィルコクソンの順位和検定を行ってみます。
を使ってウィルコクソンの順位和検定を行ってみます。
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 26 | 30 |
| 2 | 32 | 35 |
| 3 | 25 | 36 |
| 4 | 20 | 28 |
| 5 | 29 | 31 |
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 3 | 6 |
| 2 | 8 | 9 |
| 3 | 2 | 10 |
| 4 | 1 | 4 |
| 5 | 5 | 7 |
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 3 | 6 |
| 2 | 8 | 9 |
| 3 | 2 | 10 |
| 4 | 1 | 4 |
| 5 | 5 | 7 |
| 合計 | 19 | 36 |
この例題では![]() であることから、
であることから、![]() となります。
となります。
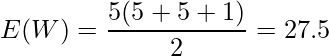
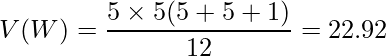
これらの値から算出したz値を用いて検定を行います。
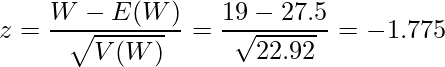
標準正規分布表より![]() となる確率(片側検定のP値)を求めると
となる確率(片側検定のP値)を求めると![]() となります。
となります。
![]() となる確率(両側検定のP値)を求めると
となる確率(両側検定のP値)を求めると![]() となります。すなわち2群間で年齢の分布に有意差があるとは言えないと結論付けられます。
となります。すなわち2群間で年齢の分布に有意差があるとは言えないと結論付けられます。
最後に、タイデータを含むデータから算出した ![]() と
と ![]() を使ってウィルコクソンの順位和検定を行ってみます。
を使ってウィルコクソンの順位和検定を行ってみます。
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 25 | 30 |
| 2 | 32 | 35 |
| 3 | 25 | 36 |
| 4 | 20 | 28 |
| 5 | 29 | 30 |
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 2.5 | 6.5 |
| 2 | 8 | 9 |
| 3 | 2.5 | 10 |
| 4 | 1 | 4 |
| 5 | 5 | 6.5 |
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 2.5 | 6.5 |
| 2 | 8 | 9 |
| 3 | 2.5 | 10 |
| 4 | 1 | 4 |
| 5 | 5 | 6.5 |
| 合計 | 19 | 36 |
この例題では![]() であることから、
であることから、![]() となります。
となります。
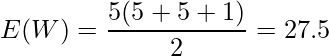
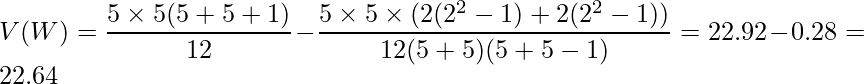
これらの値から算出したz値を用いて検定を行います。
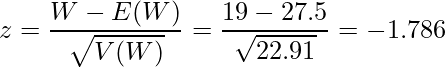
![]() となる確率(両側検定のP値)を求めると
となる確率(両側検定のP値)を求めると![]() となります。
となります。
■並べ替え検定(permutation test)
すべてのデータを使って並び替えて得られた全ての組み合わせのうち、元データの組み合わせの平均値の差より大きな値が得られる確率を算出し、この確率を元に検定を行う方法です。データにタイデータを含んでいてもいなくても、計算方法は変わりません。
次のデータを使って並べ替え検定を行ってみます。
| No. | Aチームの年齢 | Bチームの年齢 |
|---|---|---|
| 1 | 26 | 28 |
| 2 | 30 | 35 |
| 3 | 25 | 36 |
全部で6個のデータを3個ずつ2群に分けるので、![]() で20通りの組み合わせが存在します。
で20通りの組み合わせが存在します。
| No. | Aチームの組み合わせ | Bチームの組み合わせ |
|---|---|---|
| 1 | 25, 26, 28 | 30, 35, 36 |
| 2 | 25, 26, 30 | 28, 35, 36 |
| 3 | 25, 26, 35 | 30, 28, 36 |
| 4 | 25, 26, 36 | 30, 35, 28 |
| 5 | 25, 28, 30 | 26, 35, 36 |
| 6 | 25, 28, 35 | 26, 30, 36 |
| 7 | 25, 28, 36 | 26, 30, 35 |
| 8 | 25, 30, 35 | 26, 28, 36 |
| 9 | 25, 30, 36 | 26, 28, 35 |
| 10 | 25, 35, 36 | 26, 28, 30 |
| 11 | 26, 28, 30 | 25, 35, 36 |
| 12 | 26, 28, 35 | 25, 30, 36 |
| 13 | 26, 28, 36 | 25, 30, 35 |
| 14 | 26, 30, 35 | 25, 28, 36 |
| 15 | 26, 30, 36 | 25, 28, 35 |
| 16 | 26, 35, 36 | 25, 28, 30 |
| 17 | 28, 30, 35 | 25, 26, 36 |
| 18 | 28, 30, 36 | 25, 26, 35 |
| 19 | 28, 35, 36 | 25, 26, 30 |
| 20 | 30, 35, 36 | 25, 26, 28 |
| No. | Aチームの組み合わせ | Bチームの組み合わせ | 平均値の差(B-A) |
|---|---|---|---|
| 1 | 25, 26, 28 | 30, 35, 36 | 7.3 |
| 2 | 25, 26, 30 | 28, 35, 36 | 6 |
| 3 | 25, 26, 35 | 30, 28, 36 | 2.7 |
| 4 | 25, 26, 36 | 30, 35, 28 | 2 |
| 5 | 25, 28, 30 | 26, 35, 36 | 4.7 |
| 6 | 25, 28, 35 | 26, 30, 36 | 1.3 |
| 7 | 25, 28, 36 | 26, 30, 35 | 0.7 |
| 8 | 25, 30, 35 | 26, 28, 36 | 0 |
| 9 | 25, 30, 36 | 26, 28, 35 | -0.7 |
| 10 | 25, 35, 36 | 26, 28, 30 | -4 |
| 11 | 26, 28, 30 | 25, 35, 36 | 4 |
| 12 | 26, 28, 35 | 25, 30, 36 | 0.7 |
| 13 | 26, 28, 36 | 25, 30, 35 | 0 |
| 14 | 26, 30, 35 | 25, 28, 36 | -0.7 |
| 15 | 26, 30, 36 | 25, 28, 35 | -1.3 |
| 16 | 26, 35, 36 | 25, 28, 30 | -4.7 |
| 17 | 28, 30, 35 | 25, 26, 36 | -2 |
| 18 | 28, 30, 36 | 25, 26, 35 | -2.7 |
| 19 | 28, 35, 36 | 25, 26, 30 | -6 |
| 20 | 30, 35, 36 | 25, 26, 28 | -7.3 |
この例題ではハイライトで示した2つの組み合わせが、観測された組み合わせのときの平均値の差B-A=6以上となる組み合わせです。
| No. | Aチームの組み合わせ | Bチームの組み合わせ | 平均値の差(B-A) |
|---|---|---|---|
| 1 | 25, 26, 28 | 30, 35, 36 | 7.3 |
| 2 | 25, 26, 30 | 28, 35, 36 | 6 |
| 5 | 25, 28, 30 | 26, 35, 36 | 4.7 |
| 11 | 26, 28, 30 | 25, 35, 36 | 4 |
| 3 | 25, 26, 35 | 30, 28, 36 | 2.7 |
| 4 | 25, 26, 36 | 30, 35, 28 | 2 |
| 6 | 25, 28, 35 | 26, 30, 36 | 1.3 |
| 7 | 25, 28, 36 | 26, 30, 35 | 0.7 |
| 12 | 26, 28, 35 | 25, 30, 36 | 0.7 |
| 8 | 25, 30, 35 | 26, 28, 36 | 0 |
| 13 | 26, 28, 36 | 25, 30, 35 | 0 |
| 9 | 25, 30, 36 | 26, 28, 35 | -0.7 |
| 14 | 26, 30, 35 | 25, 28, 36 | -0.7 |
| 15 | 26, 30, 36 | 25, 28, 35 | -1.3 |
| 17 | 28, 30, 35 | 25, 26, 36 | -2 |
| 18 | 28, 30, 36 | 25, 26, 35 | -2.7 |
| 10 | 25, 35, 36 | 26, 28, 30 | -4 |
| 16 | 26, 35, 36 | 25, 28, 30 | -4.7 |
| 19 | 28, 35, 36 | 25, 26, 30 | -6 |
| 20 | 30, 35, 36 | 25, 26, 28 | -7.3 |
全ての組み合わせ20通りのうち、>観測された組み合わせ以上に差が大きくなる組み合わせは2通りなので、片側検定の場合のP値は次のように計算できます。
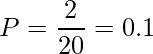
したがって、両側検定の場合のP値は![]() となります。すなわち2群間で年齢の分布に有意差があるとは言えないと結論付けられます。
となります。すなわち2群間で年齢の分布に有意差があるとは言えないと結論付けられます。
6. ノンパラメトリック検定
- 6-1. ノンパラメトリック検定とは
- 6-2. ノンパラメトリック検定 – 順位相関係数
- 6-3. ノンパラメトリック検定 – 対応のない2標本の差の検定
- 6-4. ノンパラメトリック検定 – 対応のある2標本の差の検定
- 6-5. ノンパラメトリック検定 – 対応のない3群以上のデータの差の検定






