- Step1. 基礎編
- 12. 累積分布関数と確率変数の期待値・分散
12-1. 累積分布関数とは
累積分布関数とは「確率変数![]() がある値
がある値![]() 以下(
以下(![]() )の値となる確率」を表す関数です。累積分布関数は、大文字の「
)の値となる確率」を表す関数です。累積分布関数は、大文字の「![]() 」を用いて「
」を用いて「![]() 」と表されます。
」と表されます。
例えばさいころを投げたときに「出る目が4以下となる確率」や「出る目が4から6の目が出る確率」といった、ある範囲の確率を求める場合があります。このような場合には「累積分布関数」を使うと非常に便利です。
■確率変数が離散型である場合
累積分布関数は「確率変数![]() のとる値が
のとる値が![]() となるまでの確率
となるまでの確率![]() を全て足し合わせたもの」です。式で表すと次のようになります。
を全て足し合わせたもの」です。式で表すと次のようになります。
| ・・・ | |||||
| ・・・ |
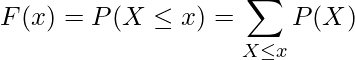
例えばさいころを投げて出る目を確率変数![]() とするとき、累積分布関数を計算すると次のようになります。
とするとき、累積分布関数を計算すると次のようになります。
| さいころの出る目 ( | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 ( |
 が1以下になる確率
が1以下になる確率 が2以下になる確率
が2以下になる確率 が3以下になる確率
が3以下になる確率 が6以下になる確率
が6以下になる確率
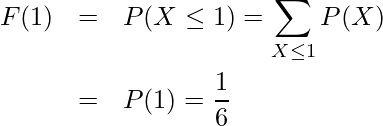
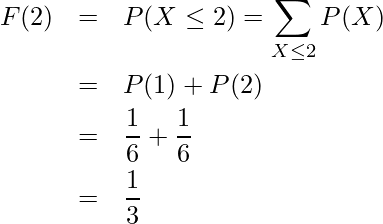
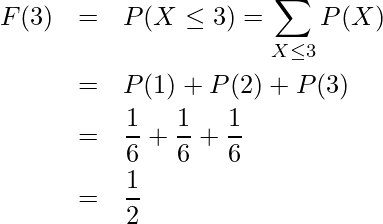
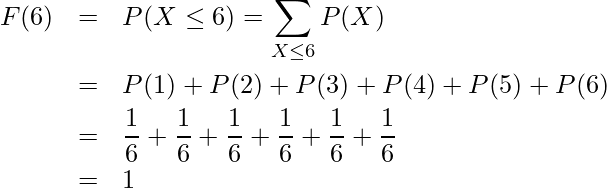
次の図は、さいころの出る目の確率とその累積分布関数を示したものです。![]() は
は![]() から
から![]() までのすべての確率を足し合わせているので、「1」になります。
までのすべての確率を足し合わせているので、「1」になります。

■確率変数が連続型である場合
累積分布関数(「確率変数![]() がある値
がある値![]() 以下
以下![]() の値となる確率」を表す関数)は、確率密度関数における
の値となる確率」を表す関数)は、確率密度関数における![]() から
から![]() までの面積と考えることができます。確率密度関数を
までの面積と考えることができます。確率密度関数を![]() とおくと、次のように確率密度関数
とおくと、次のように確率密度関数![]() の積分によって累積分布関数を求めることができます。
の積分によって累積分布関数を求めることができます。
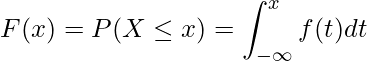
次の図は、2種類の確率密度関数とその累積分布関数を図示したものです。

【コラム】f(x)とF(x)
一般に、確率密度関数(=確率変数![]() がある値
がある値![]() となる確率密度を表す関数)は小文字の「
となる確率密度を表す関数)は小文字の「![]() 」を用いて
」を用いて![]() と表されます。一方、累積分布関数(=確率変数
と表されます。一方、累積分布関数(=確率変数![]() が
が![]() 以下となる確率を表す関数)は確率密度関数と区別するため、大文字の「
以下となる確率を表す関数)は確率密度関数と区別するため、大文字の「![]() 」を用いて
」を用いて![]() と表されます。
と表されます。
確率変数が連続型である場合、累積分布関数![]() は確率密度関数
は確率密度関数![]() を積分することで求められます。逆に、確率密度関数
を積分することで求められます。逆に、確率密度関数![]() は累積分布関数
は累積分布関数![]() を微分することで求めることができます。
を微分することで求めることができます。
■おすすめ書籍
箸休めにどうぞ。
12. 累積分布関数と確率変数の期待値・分散
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 11. 確率変数と確率分布
11-2. 離散型確率分布と確率質量関数
- 11. 確率変数と確率分布
11-3. 連続型確率分布
- 11. 確率変数と確率分布
11-5. 連続型確率分布と確率1







