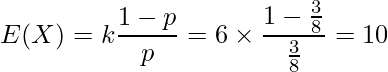- Step1. 基礎編
- 13. いろいろな確率分布1
13-8. 負の二項分布
■負の二項分布
【定義1】成功確率が![]() である独立なベルヌーイ試行を繰り返す時、
である独立なベルヌーイ試行を繰り返す時、![]() 回成功するまでの失敗回数
回成功するまでの失敗回数![]() が従う確率分布を「負の二項分布」といいます。確率変数
が従う確率分布を「負の二項分布」といいます。確率変数![]() が負の二項分布に従う場合、成功確率が
が負の二項分布に従う場合、成功確率が![]() の試行において、
の試行において、![]() 回成功するまでに
回成功するまでに![]() 回失敗する確率(
回失敗する確率(![]() となる確率)は次の式から計算できます。
となる確率)は次の式から計算できます。
![]()
例えば、歪みのないコインを投げて表が3回出るまでに裏が2回出る確率は ![]() を使って、次のように計算できます。
を使って、次のように計算できます。
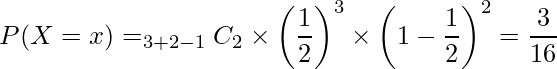

【定義2】成功確率が![]() である独立なベルヌーイ試行を繰り返す時、
である独立なベルヌーイ試行を繰り返す時、![]() 回成功するまでの試行回数
回成功するまでの試行回数![]() が従う確率分布を「負の二項分布」と定義する場合もあります。確率変数
が従う確率分布を「負の二項分布」と定義する場合もあります。確率変数![]() が負の二項分布に従う場合、成功確率が
が負の二項分布に従う場合、成功確率が![]() の試行において、
の試行において、![]() 回成功するまでに
回成功するまでに![]() 回試行する確率(
回試行する確率(![]() となる確率)は次の式から計算できます。
となる確率)は次の式から計算できます。
![]()
定義2では、![]() である場合、負の二項分布は幾何分布と等しくなります。
である場合、負の二項分布は幾何分布と等しくなります。
■例題1:
サイコロを投げて1が3回が出るまでに1以外が3回出る確率はいくらでしょうか。

成功確率は ![]() 、成功回数は
、成功回数は ![]() 、失敗回数は
、失敗回数は ![]() であることから、
であることから、
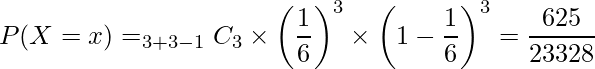
と計算できます。
■例題2:
サイコロを投げて1が3回が出るまでにサイコロを5回投げる確率はいくらでしょうか。

成功確率は ![]() 、成功回数は
、成功回数は ![]() 、試行回数は
、試行回数は ![]() であることから、
であることから、
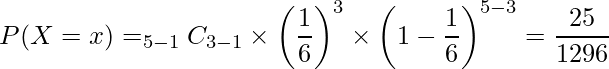
と計算できます。
■負の二項分布の期待値と分散
確率変数![]() が負の二項分布に従っている時、その期待値
が負の二項分布に従っている時、その期待値![]() と分散
と分散![]() は以下のようになります。
は以下のようになります。
<定義1>
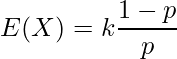
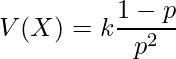
<定義2>
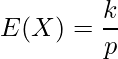
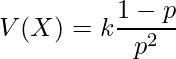
定義2では、![]() の場合に幾何分布における期待値と分散に等しくなることが分かります。定義1には成功回数
の場合に幾何分布における期待値と分散に等しくなることが分かります。定義1には成功回数![]() が確率変数
が確率変数![]() には含まれていないので、
には含まれていないので、![]() を加えると
を加えると![]() の期待値は
の期待値は![]() となり、定義2の期待値に等しくなります。
となり、定義2の期待値に等しくなります。
■例題3:
赤玉が5個、白玉が3個入った袋から玉を1つ取り出し、取り出した玉を再び袋に戻すという試行を行う場合、白玉が6回出るまでの失敗(赤玉が取り出される)回数の期待値はいくらでしょうか。

定義1の期待値の式を使って次のように計算できます。