- Step1. 基礎編
- 27. 回帰分析
27-5. 決定係数と重相関係数
■決定係数
決定係数はデータに対する、推定された回帰式の当てはまりの良さ(度合い)を表します。決定係数は一般に![]() で示され、0から1までの値をとります。1に近いほど、回帰式が実際のデータに当てはまっていることを表しており、説明変数が目的変数をよく説明していると言えます。
で示され、0から1までの値をとります。1に近いほど、回帰式が実際のデータに当てはまっていることを表しており、説明変数が目的変数をよく説明していると言えます。
■決定係数の例
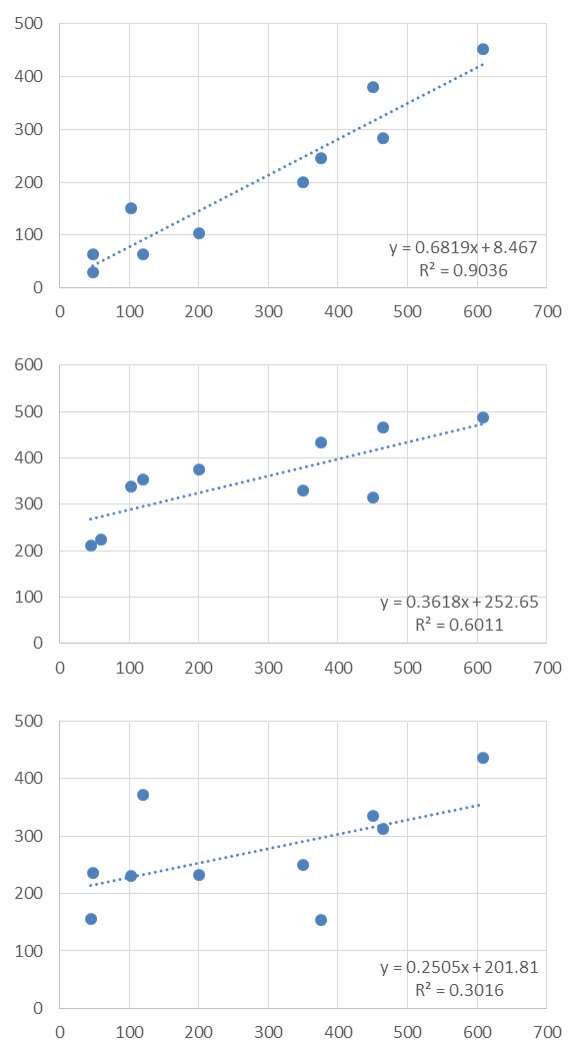
いくつかの単回帰式とその決定係数を見てみます。決定係数は上から順に「0.9」「0.6」「0.3」です。
■決定係数の求め方
決定係数を求めるにためには、実際のデータと推定された回帰式から「全変動」「回帰変動」「残差変動」の3つを求める必要があります。ここでは実際のデータを(![]() )、回帰式から推定されたデータを(
)、回帰式から推定されたデータを(![]() )、データ全体から求められる平均値を(
)、データ全体から求められる平均値を(![]() )とします。
)とします。
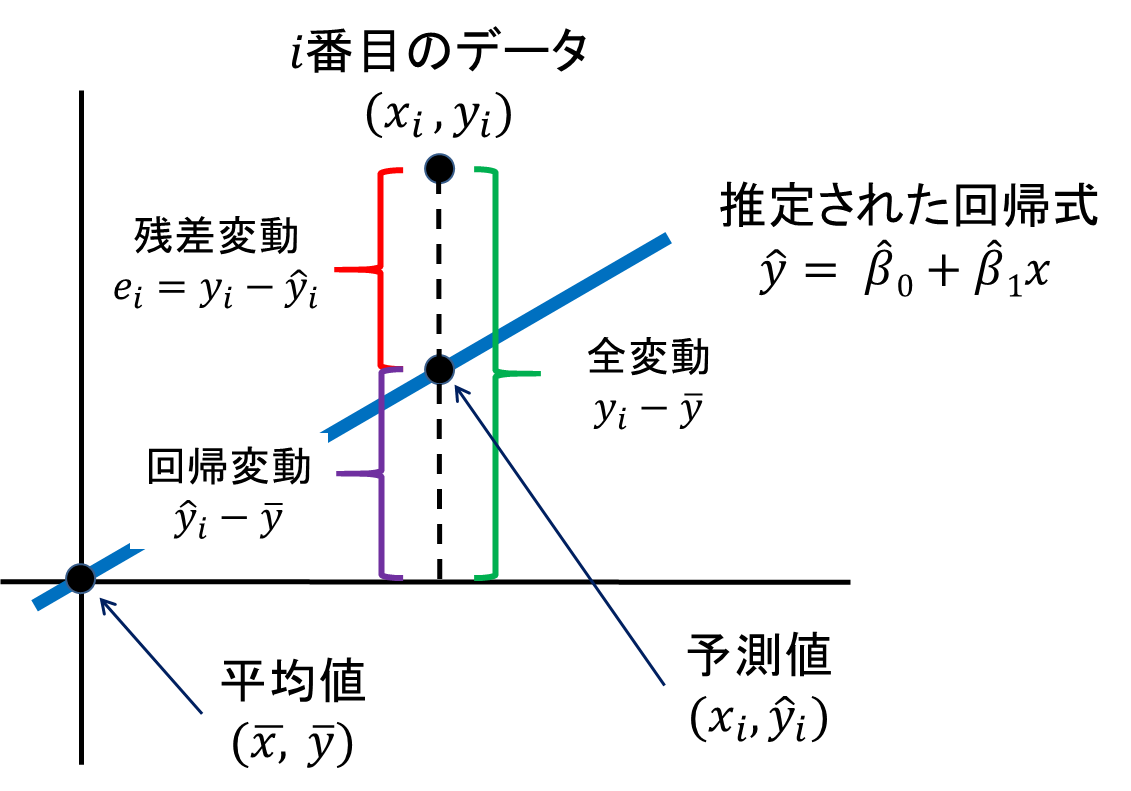
- 「全変動」:実際のデータとデータ全体の平均値との差を表します(上の図の緑の部分)
- 「回帰変動」:推定された回帰式から得られた予測値とデータ全体の平均値の差を表します(上の図の紫の部分)
- 「残差変動」:実際のデータと推定された回帰式から得られた予測値との差を表します(上の図の赤の部分)
これらの変動は二乗和として算出します。
| 変動 | 計算式 |
|---|---|
| 全変動の平方和 |
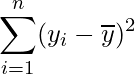 |
| 回帰変動の平方和 |
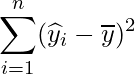 |
| 残差変動の平方和 |
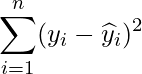 |
上の図から、
という式が成り立つことが分かります。この式をもう少し詳しく書くと次のようになります。
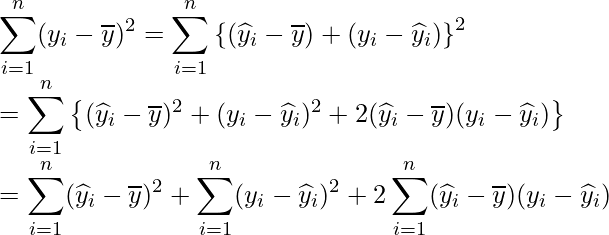
次に、![]() を展開します。以下の式が成り立つので、
を展開します。以下の式が成り立つので、
この式を代入します。
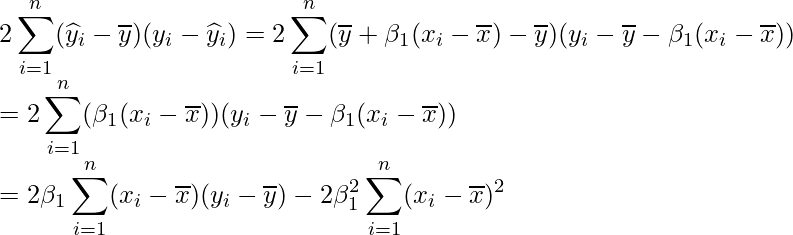
![]() は次の式で表すことができます(詳しくは27-1章をご覧ください)。
は次の式で表すことができます(詳しくは27-1章をご覧ください)。
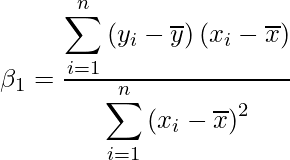
この式を代入すると
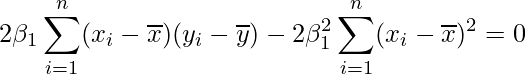
となります。したがって、次の式が成り立ちます。
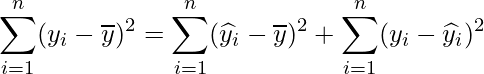
決定係数は、説明変数が目的変数をどれくらい説明しているか、つまり「回帰変動が全変動に対してどれだけ多いか=残差変動が全変動に対してどれだけ少ないか」を表すものです。したがって決定係数は、次に示すように回帰変動を全変動で割ることで求められます。
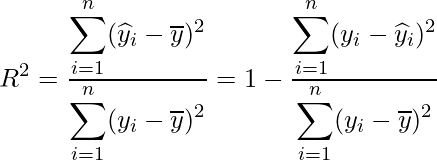
27‐2章で示した次のデータの場合、決定係数は「0.55」となりました。この結果は、4つの説明変数を用いた回帰モデルによって目的変数の約55%を説明できるということを示しています。
■自由度調整済み決定係数
決定係数は説明変数の数が増えるほど1に近づくという性質を持っています。そのため、説明変数の数が多い場合には、この点を補正した「自由度調整済み決定係数(自由度修正済み決定係数)」を使います。自由度調整済み決定係数は次の式から求められます。nはサンプルサイズを、kは説明変数の数を表します。
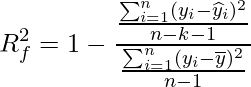
27‐2章で示した次のデータの場合、決定係数は「0.55」、自由度調整済み決定係数は「0.51」となり、変数の数の影響が調整された自由度調整済み決定係数のほうが決定係数に比べて小さくなっていることが分かります。
決定係数や自由度調整済み決定係数を用いると、異なる回帰モデル間での良し悪しを判断することができます。特に、説明変数の数が異なる回帰モデルどうしを比較する場合には、自由度調整済み決定係数を使います。決定係数や自由度調整済み決定係数の値が高いほど、元のデータに対する当てはまりが良いモデルであると言えます。
■重相関係数
実際に観測された目的変数の値と、重回帰式をあてはめて計算した推定値(理論値)との相関係数です。重相関係数は一般に![]() で示され、0から1の間の値を取ります。1に近いほど分析の精度は高いと言えます。
で示され、0から1の間の値を取ります。1に近いほど分析の精度は高いと言えます。
27. 回帰分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
決定係数
- ブログ
回帰係数と相関係数
- ブログ
Excelで重回帰分析(1)
- ブログ
重回帰分析ができない







