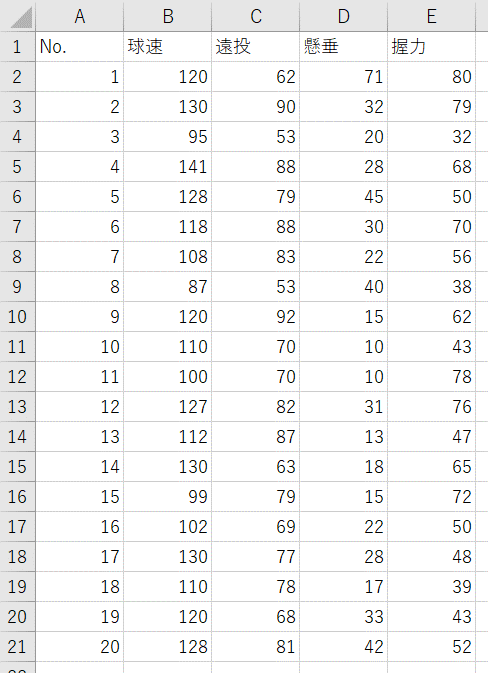
次のデータは「重回帰分析─エクセル統計による解析事例」に掲載している野球選手の体力測定の結果です。このデータを使って「回帰分析」を行ってみます。

分析ツールから「回帰分析」を選択し、ウィンドウを次のように設定します。

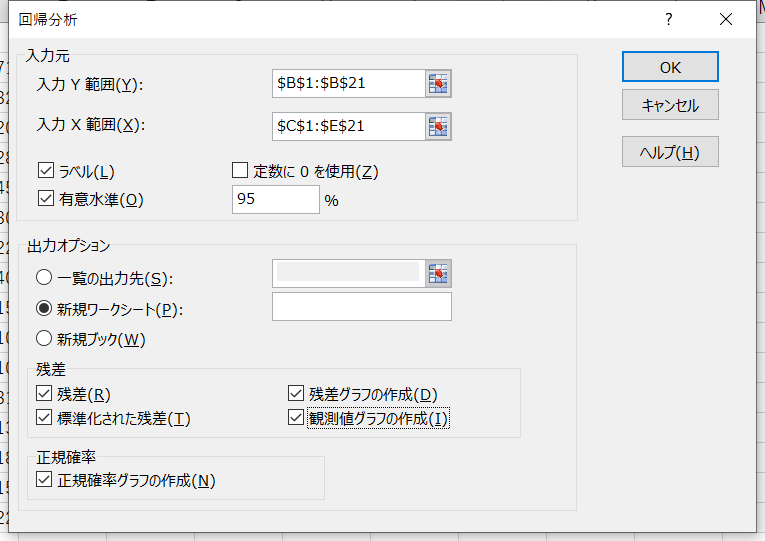
【オプションの説明】

• 入力Y範囲：目的変数のデータ範囲
• 入力X範囲：説明変数のデータ範囲
• ラベル：入力範囲にラベル（列名）を含む場合はチェックする
• 定数に0を使用：切片が0の場合にはチェックする
• 有意水準：偏回帰係数の信頼区間を出力する場合に使用（チェックを入れなかった場合でも95%信頼区間は自動的に出力される）
• 一覧の出力先：指定したセルに結果を出力する場合に使用
• 新規ワークシート：新規ワークシートに結果を出力する場合に使用
• 新規ブック：新規ブックに結果を出力する場合に使用
• 残差：観測値から予測値（回帰式により算出された値）を引いた結果を出力する場合に使用
• 標準化された残差：標準化した残差の値を出力する場合に使用
• 残差グラフの作成：残差グラフ（ある説明変数と残差をプロットしたもの）を出力する場合に使用
• 観測値グラフの作成：説明変数の値に対する目的変数の値、及び予測値のプロットを出力する場合に使用
• 正規確率グラフの作成：正規確率グラフ（目的変数を小さい順に並べたときの百分率と目的変数の値をプロットしたもの）を出力する場合に使用

すると、左側に回帰分析の結果が表示されます。

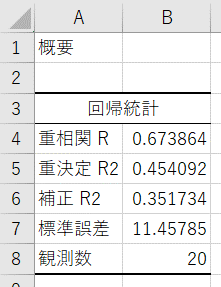
【結果の説明（回帰統計）】

• 重相関R：重相関係数。実際に観測された目的変数の値と、回帰式をあてはめて計算した推定値（理論値）との相関係数。重相関係数は、0から1の間の値を取り、1に近いほど分析の精度は高いと言える。
• 重決定R2：決定係数。推定された回帰式の当てはまりの良さ（度合い）を表す。決定係数は0から1までの値をとり、1に近いほど回帰式が実際のデータに当てはまっている（説明変数が目的変数をよく説明している）ことを表す。
• 補正R2：自由度調整済み決定係数。説明変数の数で補正した決定係数。
• 標準誤差：分散分析表の「残差の分散」の二乗根。重回帰分析による目的変数の推定値が観測値がに対してどの程度散らばっているのかを表す。
• 観測数：データの数

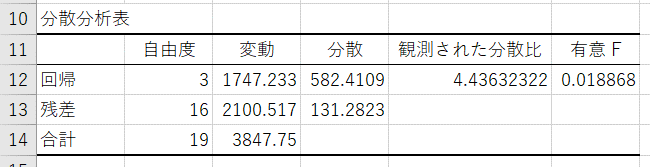
【結果の説明（分散分析表）】

「母重相関係数は 0（ゼロ）である」という帰無仮説の検定結果を表す。この検定は、全ての偏回帰係数が0であるかどうかを検定するものであり、この検定結果が有意である場合には、この回帰式は意味があると言える。

【結果の説明（偏回帰係数）】

• 係数：偏回帰係数
• 標準誤差：偏回帰係数の標準誤差
• t：偏回帰係数を標準誤差で割った値
• P-値：t値に対する検定結果。自由度（n-k-1）のt分布を用いて検定う。nはサンプルサイズを、kは説明変数の数を表す。
• 下限95%：偏回帰係数の信頼区間の下端の値
• 上限95%：偏回帰係数の信頼区間の上端の値

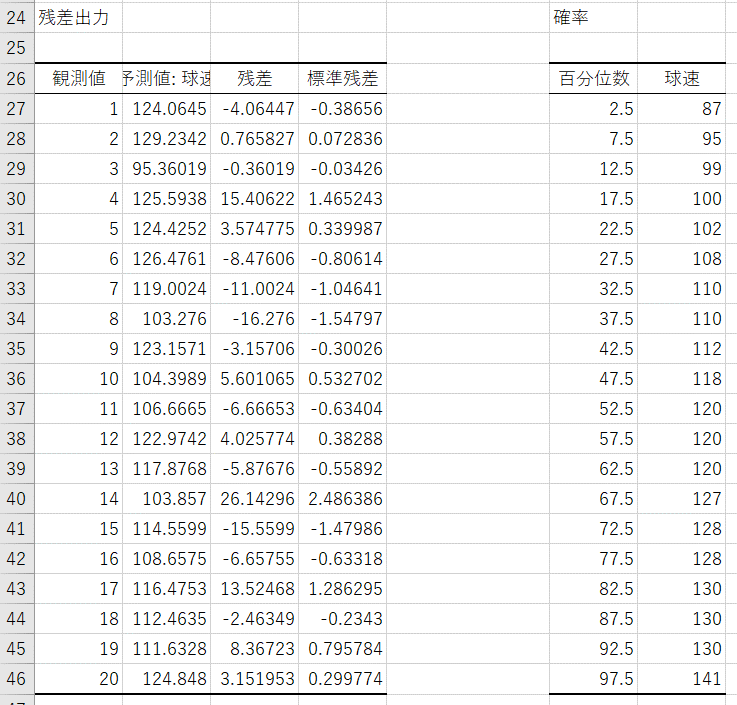
【結果の説明（その他）】

• 観測値：目的変数の通し番号。入力した目的変数に対して、上から1, 2, 3…という値がつけられる。
• 予測値：回帰分析によって算出された予測値
• 残差：観測値から予測値を引いたもの
• 標準残差：残差の値を標準化したもの
• 百分位数：目的変数を小さい順に並べたたときの百分率
• 目的変数名：百分位数に対する目的変数の値

右側には様々なグラフが表示されます。

【結果の説明（残差グラフ）】

説明変数の値と残差の値をプロットしたもの。回帰式がデータに対して妥当であれば残差は適当にばらつくことが予想される。したがって、残差が偏っていないか、何らかの傾向がないか（だんだん増加している、減少している等）についてチェックするために残差グラフを確認する。

【結果の説明（観測値グラフ）】

説明変数の値と目的変数の値（観測値と予測値）をプロットしたもの。回帰分析の結果、観測値と予測値がどの程度近いかをチェックすることができる。両者のプロットが近い場合には、回帰式が妥当であると考えられる。

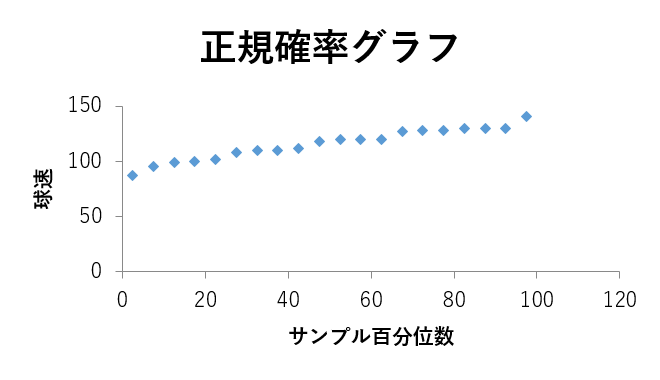
【結果の説明（正規確率プロット）】

目的変数の百分率と目的変数の値をプロットしたもの。データの分布が正規分布に従っているかどうかを調べることができる。プロットが一直線上に並んでいれば正規分布に従っていると考えられる。

■ブログで連載していたコラム「Excelで重回帰分析」もあわせてご覧ください。

• Excelで重回帰分析(1)
• Excelで重回帰分析(2)
• Excelで重回帰分析(3)―標準偏回帰係数
• Excelで重回帰分析(4)―重相関係数と決定係数
• Excelで重回帰分析(5)―自由度調整済み決定係数
• Excelで重回帰分析(6)―重回帰分析の分散分析とt検定