- Excelノート
- 統計検定 データサイエンス基礎のための分析ツールの使い方
2-1. 分析ツール t検定・z検定
Excelには統計解析を便利に行うための「分析ツール」が入っています。この章ではこの分析ツールの使い方について説明します。下記のリンクからそれぞれの解説に飛ぶことができます。
- 分析ツールの導入方法
- t検定とz検定のまとめ
- t 検定:一対の標本による平均の検定
- t 検定:等分散を仮定した2標本による検定
- t 検定:分散が等しくないと仮定した2標本による検定
- z 検定:2標本による平均の検定
分析ツールの導入方法
分析ツールはExcelの「データ」タブ内の右端にある「データ分析」をクリックすると使うことができます。

もし「データ分析」が見当たらない場合は、次の手順に従って「分析ツールアドイン」を追加する必要があります。
- Excelの「ファイル」タブを選択する
- 左側の項目から「オプション」を選択する
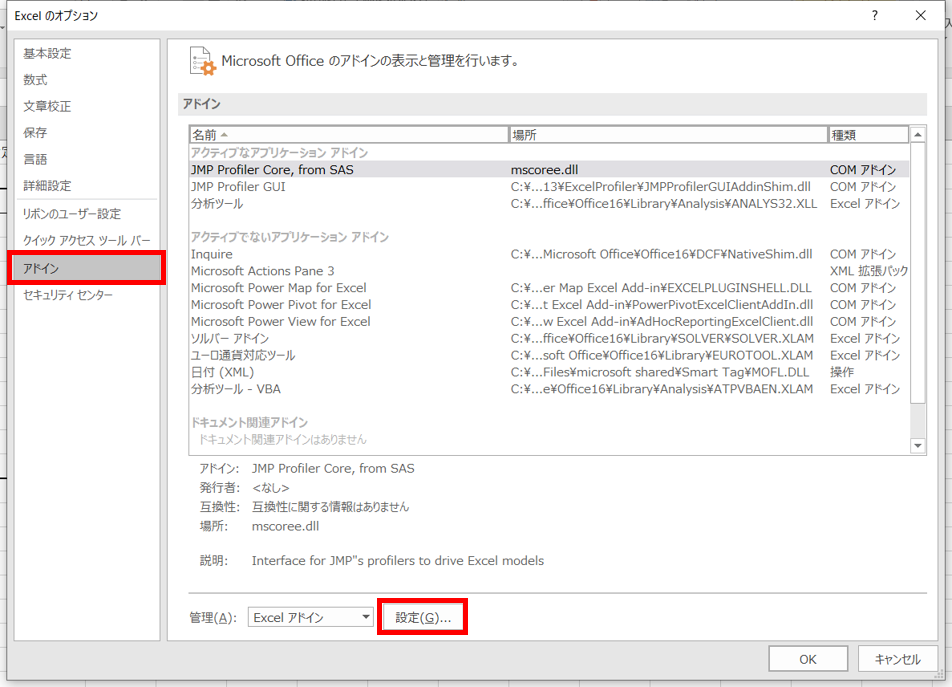
- 左側の項目から「アドイン」を選択し、さらに下中央にある「設定」をクリックする
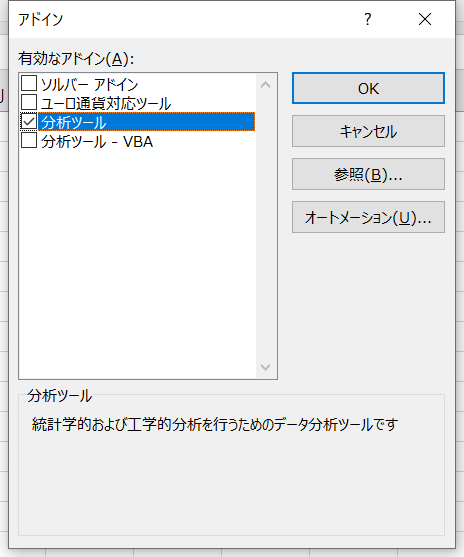
- 「分析ツール」にチェックを入れ、「OK」をクリックする
- Excelを再起動する

t検定とz検定のまとめ
| 分析ツール名 | 使い方 | 関連リンク |
|---|---|---|
| t 検定:一対の標本による平均の検定 | 対応のある2標本の平均値の差の検定(母分散未知) | 24-5. 対応のある2標本t検定 |
| t 検定:等分散を仮定した2標本による検定 | 対応のない2標本の母分散が等しいと仮定できる場合の平均値の差の検定(母分散未知) | 24-4. 対応のない2標本t検定 |
| t 検定:分散が等しくないと仮定した2標本による検定 | 対応のない2標本の母分散が等しいと仮定できない場合の平均値の差の検定(母分散未知) | 28-4. Welchのt検定 |
| z 検定:2標本による平均の検定 | 2標本の平均値の差の検定(母分散既知) | - |
t 検定:一対の標本による平均の検定
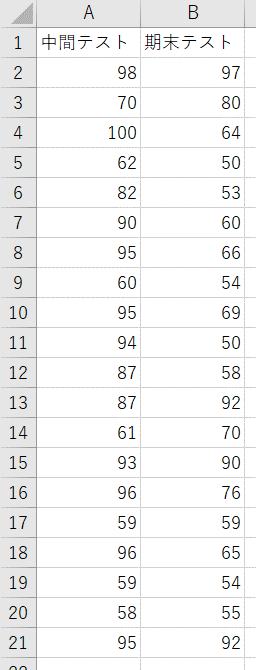
次のデータは、あるクラスの数学の中間テストと期末テストの結果です。このデータを使って、平均値に差があるかどうかを検定してみます。このデータのように同一のサンプルから取得されたデータを比較する場合には「一対の標本による平均の検定(対応のある2標本t検定)」を使います。
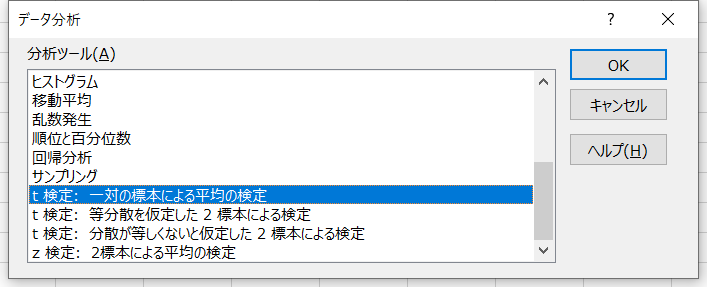
分析ツールから「t 検定:一対の標本による平均の検定」を選択し、ウィンドウを次のように設定します。
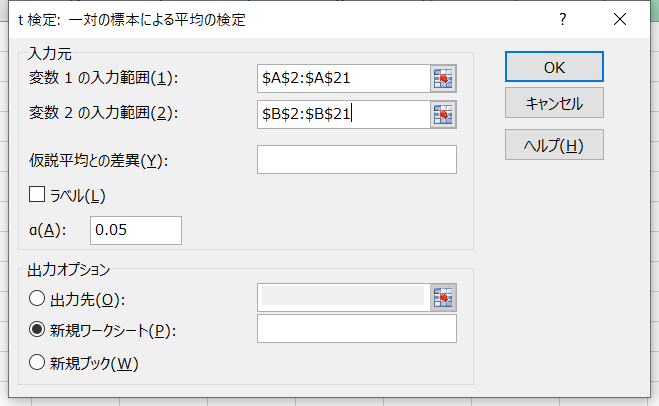
【オプションの説明】
- 変数1の入力範囲:1つ目のデータの範囲
- 変数2の入力範囲:2つ目のデータの範囲
- 仮説平均との差異:空欄もしくは「0」を入力
- ラベル:入力範囲にラベル(列名)を含む場合はチェックする
- α:有意水準
- 出力先:指定したセルに結果を出力する場合に使用
- 新規ワークシート:新規ワークシートに結果を出力する場合に使用
- 新規ブック:新規ブックに結果を出力する場合に使用
すると、結果が表示されます。
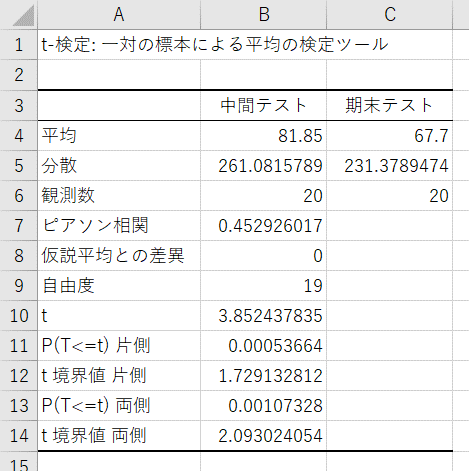
【結果の説明】
- 平均:各データの平均値
- 分散:各データの不偏分散
- 観測数:各データのサンプルサイズ
- ピアソン相関:2つのデータのピアソン積率相関係数
- 仮説平均との差異:仮説平均との差異に設定した値
- 自由度:サンプルサイズ-1
- t:データから算出されたt値
- P(T<=t)片側:片側検定の場合のP値
- t境界値 片側:片側検定の場合の棄却限界値(この値をt値が超えると有意)
- P(T<=t)両側:両側検定の場合のP値
- t境界値 両側:両側検定の場合の棄却限界値(この値をt値が超えると有意)
両側検定のP値が0.00107なので、中間テストと期末テストの点数に有意差があると結論付けられます。
t 検定:等分散を仮定した2標本による検定
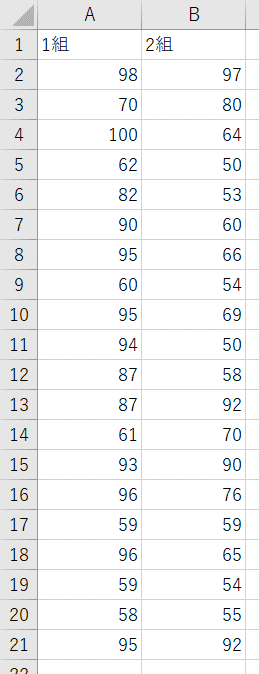
次のデータは、1組と2組の数学のテストの結果です。このデータを使って、平均値に差があるかどうかを検定してみます。このデータのように異なるサンプルから取得されたデータを比較する場合で、それぞれのデータの母分散が等しいと仮定できる場合には「2標本による検定(対応のない2標本t検定)」を使います。
分析ツールから「t 検定:一対の標本による平均の検定」を選択し、ウィンドウを次のように設定します。
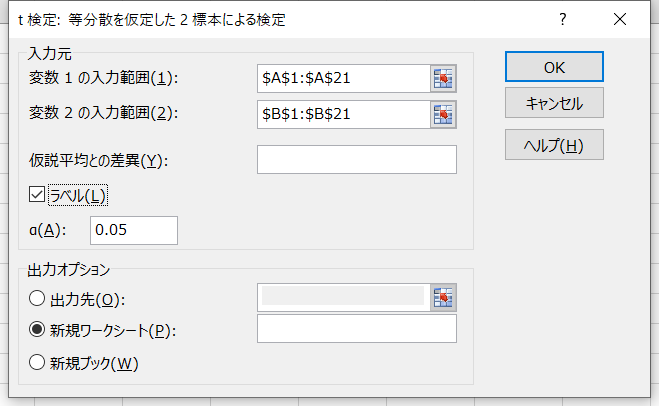
すると、結果が表示されます。
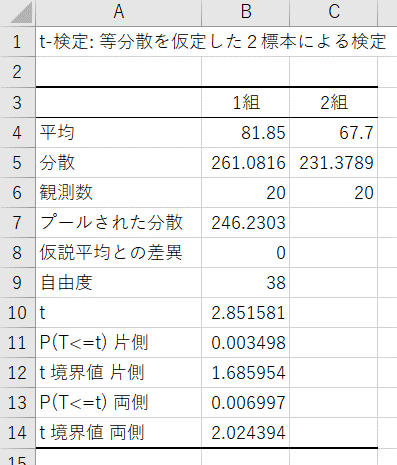
【結果の説明】
- 平均:各データの平均値
- 分散:各データの不偏分散
- 観測数:各データのサンプルサイズ
- プールされた分散:2つのデータの分散を併合した値
- 仮説平均との差異:仮説平均との差異に設定した値
- 自由度:(1つ目のデータのサンプルサイズ-1)+(2つ目のデータのサンプルサイズ-1)
- t:データから算出されたt値
- P(T<=t)片側:片側検定の場合のP値
- t境界値 片側:片側検定の場合の棄却限界値(この値をt値が超えると有意)
- P(T<=t)両側:両側検定の場合のP値
- t境界値 両側:両側検定の場合の棄却限界値(この値をt値が超えると有意)
両側検定のP値が0.00700なので、1組と2組のテストの点数に有意差があると結論付けられます。
t 検定:分散が等しくないと仮定した2標本による検定
「2標本による検定(対応のない2標本t検定)」とは異なり、それぞれのデータの母分散が等しいと仮定できない場合(あるいは分からない場合)には「t 検定:分散が等しくないと仮定した2標本による検定(Welchのt検定)」を使います。
Welchの方法ではt分布の自由度に小数点を含む値が出てきます。しかしExcelの分析ツールでは、四捨五入した整数値の自由度によるt分布を用いてP値を計算するため、R等の出力結果とは異なります。もし、小数点を含む自由度をそのまま用いてt検定(Welchのt検定)を行いたい場合には、ExcelのTTEST関数やT.TEST関数を使うようにしてください。詳しくはこちらをご覧ください。
z 検定:2標本による平均の検定
z検定は母分散が既知の場合に、2つのデータの平均値に差があるかどうかを検定する場合に使います。ただし、母分散が既知である状況は現実的には無いため、z検定を使う機会は殆どありません。
統計検定 データサイエンス基礎のための分析ツールの使い方
- 2-1. 分析ツール t検定・z検定
- 2-2. 分析ツール 基本統計・相関・ヒストグラム
- 2-3. 分析ツール 回帰分析
- 2-4. 分析ツール 分散分析:一元配置、二元配置
- 2-5. 分析ツール 乱数発生・順位と百分位数・サンプリング






