- Step1. 基礎編
- 27. 回帰分析
27-6. 回帰の有意性の検定
27-3章で、偏回帰係数の有意性の検定について学びました。回帰分析においてある説明変数の偏回帰係数が0である(目的変数に対して効果がある)かを検定する場合には、t分布を用いて偏回帰係数の有意性の検定を行います。一方、複数の説明変数における回帰係数の効果を同時に検定する(回帰式そのものが目的変数に対して効果があるかを検定する)場合にはF分布を用いて回帰の有意性の検定を行います。
■回帰の有意性の検定とは
複数の説明変数における回帰係数![]() の効果を同時に検定する場合、帰無仮説
の効果を同時に検定する場合、帰無仮説![]() と対立仮説
と対立仮説![]() は次のように書けます。
は次のように書けます。
回帰式そのものの目的変数に対する効果の検定には、27-5章で学んだ「変動」を活用します。すなわち、「回帰変動の平方和(SSR: Sum of Squared Regression)」と「残差変動の平方和(SSE: Sum of Squared Error)」をそれぞれ自由度「![]() 」と「
」と「![]() 」で割った平均平方を用います。
」で割った平均平方を用います。![]() は説明変数の数を、
は説明変数の数を、![]() はデータの数を表します。
はデータの数を表します。
「回帰変動の平均平方」と「残差変動の平均平方」をそれぞれMSR(mean squared regression)、MSE(mean squared error)とすると、
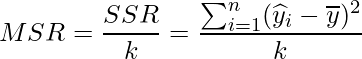

となります。ただし、実際のデータを![]() 、回帰式から推定された値を
、回帰式から推定された値を![]() 、データ全体から求められる平均値を
、データ全体から求められる平均値を![]() とします。
とします。
「回帰変動の平均平方」と「残差変動の平均平方」の比である ![]() が自由度
が自由度 ![]() のF分布に従うことを利用して検定を行います。
のF分布に従うことを利用して検定を行います。
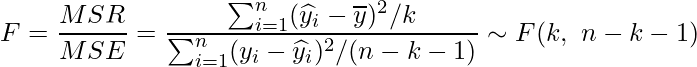
この検定では、残差変動の平均平方(残差変動のばらつき)に対する回帰変動の平均平方(回帰変動のばらつき)が相対的に大きいかどうかを検定します。大きい場合には回帰変動による効果は有意である(回帰式そのものが目的変数に対して効果がある=偏回帰係数のいずれかが0ではない)と判断できますが、小さい場合には回帰変動による効果は有意であるとはいえません。有意ではない場合には、得られた回帰式にはあまり意味がありません。
回帰変動のばらつきが相対的に大きいかどうかだけを見ればよいので、この検定では「片側検定」を行います。
※F分布を用いた検定の詳細については28章以降で詳しく触れます。
■分散分析表
回帰の有意性の検定を行う際には、次のような分散分析表を作成する場合があります。![]() は説明変数の数を、
は説明変数の数を、![]() はデータの数を表します。
はデータの数を表します。
| 要 因 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 回帰変動 | 回帰変動の平方和 (SSR) |
回帰変動の平均平方 (MSR) |
||
| 残差変動 | 残差変動の平方和 (SSE) |
残差変動の平均平方 (MSE) |
- | |
| 全体変動 | 全変動の平方和 (SST) |
- | - |
※分散分析の詳細については28章以降で詳しく触れます。







