- 数学ノート
- 統計学で使う数学
対数(log)
■対数とは
![]() を
を ![]() 乗したものが
乗したものが ![]() になる場合、この
になる場合、この ![]() のことを 「
のことを 「![]() を底(てい)とする
を底(てい)とする ![]() の対数」といいます。また、
の対数」といいます。また、![]() を真数(しんすう)といいます。
を真数(しんすう)といいます。
対数と指数の関係を表すと次のようになります。ただし、![]() は1以外の正の値(
は1以外の正の値(![]() 、
、![]() )を、
)を、![]() は正の値(
は正の値(![]() )をとります。
)をとります。
例えば、「2の3乗は8(![]() )」を対数を使って表すと次のようになります。
)」を対数を使って表すと次のようになります。
このように、対数は指数を使って表すような大きな数を扱う際にとても便利です。対数の特別な場合として、![]() の 1乗は
の 1乗は ![]() (
(![]() )なので
)なので
となります。また![]() の 0乗は 1(
の 0乗は 1(![]() )なので
)なので
となります。
■対数の公式
対数には次に示す「対数の公式」が成り立ちます(ただし ![]() 、
、![]() 、
、![]() 、
、![]() とします)。
とします)。
例えば ![]() は
は
と計算できます。
【証明】![]() 、
、![]() とおきます。このとき、
とおきます。このとき、![]() 、
、![]() となります。
となります。
![]() を底とする対数を取ると、
を底とする対数を取ると、
となります。
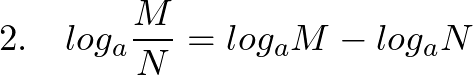
例えば ![]() は
は
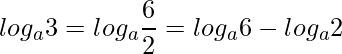
と計算できます。
【証明】![]() 、
、![]() とおきます。このとき、
とおきます。このとき、![]() 、
、![]() となります。
となります。
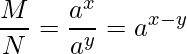
![]() を底とする対数を取ると、
を底とする対数を取ると、
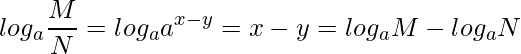
となります。
例えば ![]() は
は
と計算できます。
【証明】![]() とおきます。このとき、
とおきます。このとき、![]() となります。両辺を
となります。両辺を ![]() 乗すると、
乗すると、
![]() を底とする対数を取ると、
を底とする対数を取ると、
となります。
■底の変換
対数の底の値は、次の式を使って変換することができます(ただし ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() とします)。
とします)。
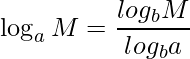
例えば ![]() について考えてみます。底が2の対数に変換すると
について考えてみます。底が2の対数に変換すると
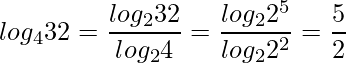
と計算できます。
【証明】![]() とおきます。このとき、
とおきます。このとき、![]() となります。
となります。![]() を底とする対数を取ると
を底とする対数を取ると
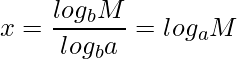
となります。
■常用対数と自然対数
底が10である対数を「常用対数」といいます。10を ![]() 乗したものが
乗したものが ![]() となるとき、
となるとき、![]() は常用対数を使って次のように表すことができます。
は常用対数を使って次のように表すことができます。
あるいは、慣例的に次のように表す場合もあります。
常用対数と使うと、大きな数の桁数を簡単に求めることができます。整数 ![]() が
が ![]() 桁であるとき
桁であるとき
と表すことができます。常用対数を取ると
となります。例えば50,000は
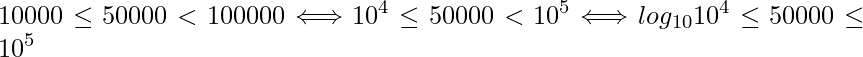
となることから、50,000は5桁の数字であることが分かります。
底が ![]() (ネイピア数)である対数を「自然対数」といいます。
(ネイピア数)である対数を「自然対数」といいます。![]() を
を ![]() 乗したものが
乗したものが ![]() となるとき、
となるとき、![]() は常用対数を使って次のように表すことができます。
は常用対数を使って次のように表すことができます。
あるいは、慣例的に次のように表す場合もあります。
【例題】
次の計算式を簡単にするとどうなるでしょうか。







