微分とはある関数の導関数を求めることです。導関数は、関数の接線の傾きを表す関数で、あるグラフと一点のみを共有する直線を表します。関数の導関数は、「」をつけて「」と表します。また、「」と表すこともあります。

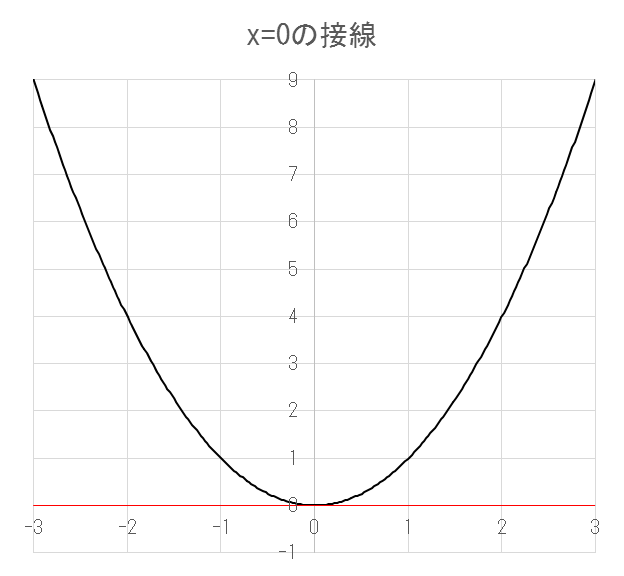
例えばy=における導関数はです。この式を用いてのにおける接線の傾きを求めてみます。導関数は、ある値xにおける接線の傾きを表しているので、にを代入すると傾きは0であることが分かります。

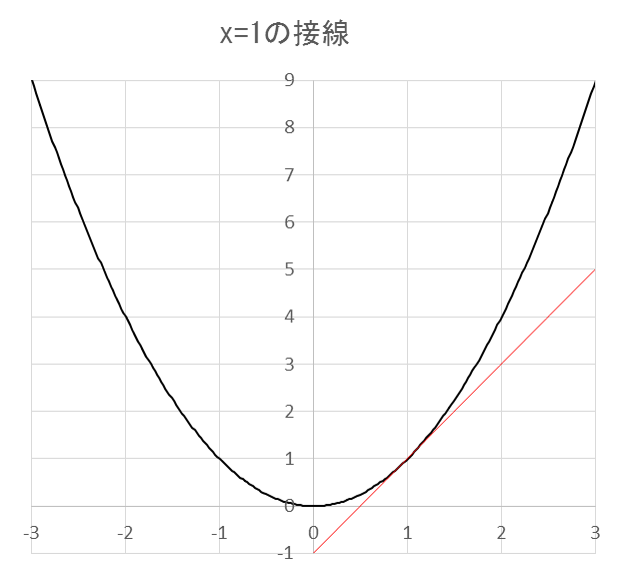
また、における接線の傾きは次の計算により2であると求められます。

とその導関数には次のような関係があります。