- 数学ノート
- 統計学で使う数学
積分の使用例
統計を学ぶ際、次のような場合に積分を計算することがあります。 いくつかの関数を例に、実際に計算した例を紹介します。
確率を計算する
例題:次の分布に従う確率変数![]() について、
について、![]() を求めてみましょう。
を求めてみましょう。
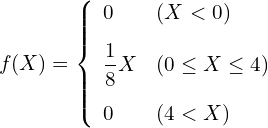
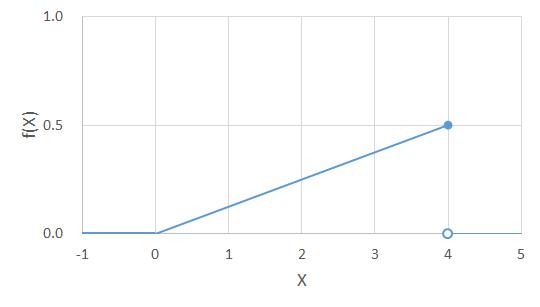
![]() のグラフは次の通りです。
のグラフは次の通りです。
解答例
![]() を0.5から2まで積分した値が答えです。
を0.5から2まで積分した値が答えです。
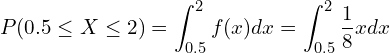
![Rendered by QuickLaTeX.com \displaystyle = \left[ \frac{1}{16} x^2 \right]_{0.5}^{2} = \frac{2^2}{16} - \frac{0.5^2}{16}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-378a72dfd34a8512be3caf3cc2a9eaac_l3.png)
期待値を計算する
例題:次の分布に従う確率変数![]() について、
について、![]() を求めてみましょう。
を求めてみましょう。
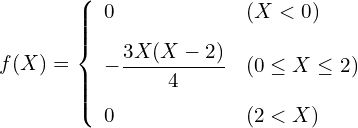
![]() のグラフは次の通りです。
のグラフは次の通りです。
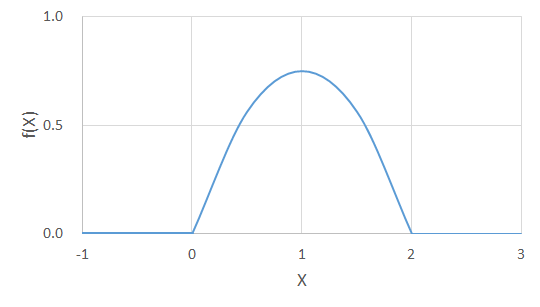
解答例
![]() を0から2まで積分した値が答えです。
を0から2まで積分した値が答えです。
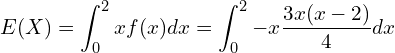
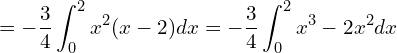
![Rendered by QuickLaTeX.com \displaystyle = -\frac{3}{4} \left[ \frac{x^4}{4} - \frac{2x^3}{3} \right]_{0}^{2} = -\frac{3}{4} \left\{ \left( 4- \frac{16}{3} \right) - \left( 0-0 \right) \right\}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-9333b9d8b837169eaad1bb7c91376c0e_l3.png)
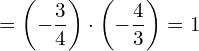
分散を計算する
例題:次の分布に従う確率変数![]() について、
について、![]() を求めてみましょう。
を求めてみましょう。
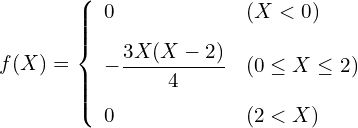
![]() のグラフは前問と同じで、次の通りです。
のグラフは前問と同じで、次の通りです。

解答例
![]() を0から2まで積分した値が答えです。直前の例題より、
を0から2まで積分した値が答えです。直前の例題より、![]() とわかっているため、
とわかっているため、![]() を計算すればよいことがわかります。
を計算すればよいことがわかります。
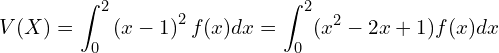
このままだと計算しにくいので、少し変形しましょう。
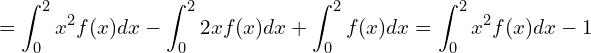
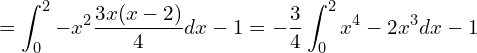
![Rendered by QuickLaTeX.com = \displaystyle -\frac{3}{4} \left[ \frac{x^5}{5}- \frac{x^4}{2} \right]_{0}^{2} -1](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-4c301c4aa68c3afc2b09db63809b1ffd_l3.png)
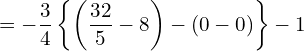
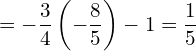
中央値を計算する
例題:次の分布に従う確率変数![]() について、中央値を求めてみましょう。
について、中央値を求めてみましょう。
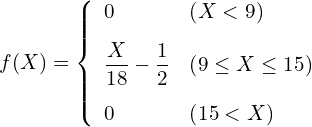
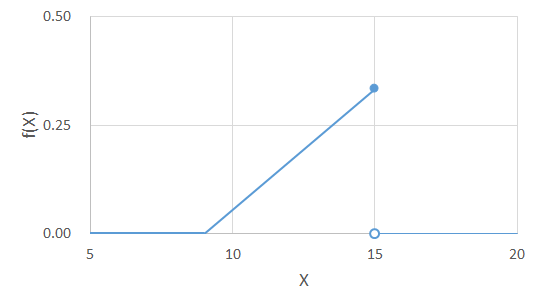
![]() のグラフは次の通りです。
のグラフは次の通りです。
解答例
![]() の累積確率
の累積確率![]() が0.5となる点を求めます。まずは、
が0.5となる点を求めます。まずは、![]() を計算します。
を計算します。
![Rendered by QuickLaTeX.com \displaystyle =\left[ \frac{t^2}{36} -\frac{t}{2} \right]_{9}^{x} = \left( \frac{x^2}{36} -\frac{x}{2} \right) -\left( \frac{81}{36} -\frac{9}{2} \right)](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-75f574b1f686a46c09b42edb729e862f_l3.png)
F(x)のグラフは次のようになります。
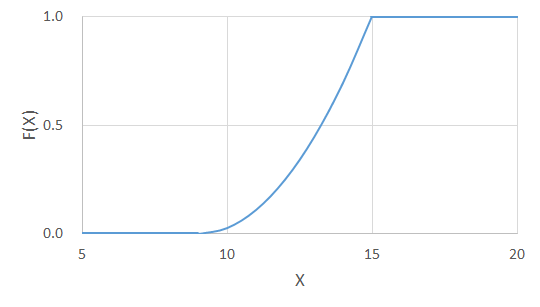
中央値は![]() となる点です。グラフ上で図示すると、赤い線とx軸が交わる点です。
となる点です。グラフ上で図示すると、赤い線とx軸が交わる点です。
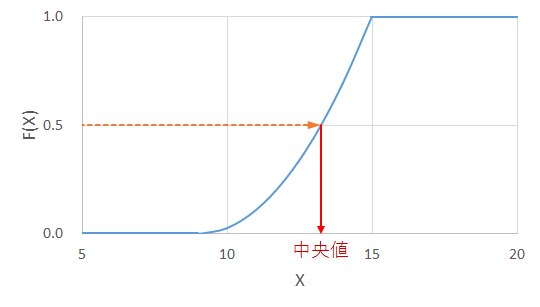
上で求めた![]() を代入すると、次の2次方程式となります。
を代入すると、次の2次方程式となります。
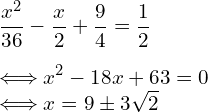
解が2つ出てきましたが、Xは![]() を満たす必要があります。このことから、
を満たす必要があります。このことから、![]() は9より小さいため不適であり、中央値は
は9より小さいため不適であり、中央値は![]() であることがわかります。
であることがわかります。






