- 数学ノート
- 統計学で使う数学
積分の計算
ある関数![]() を積分する際に、
を積分する際に、![]() といった具体的な区間が与えられた場合には、
といった具体的な区間が与えられた場合には、
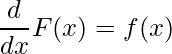
![Rendered by QuickLaTeX.com \displaystyle \int_a^b{f(x)dx}=[F(x)]_a^b=F(b)-F(a)](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b99fe6dfdc33c70ce2b836c5e4674b8d_l3.png)
次に、この![]() を求めるための公式を紹介します。
を求めるための公式を紹介します。
■xnの積分公式
![]() の形で表される関数の積分は、次のように計算できます。
の形で表される関数の積分は、次のように計算できます。
![Rendered by QuickLaTeX.com \displaystyle \int_{a}^{b} x^n dx=\left[\frac{1}{n+1} {x}^{n+1} \right]_{a}^{b}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b29ed44c14ba838c608adc9cc2adb9ff_l3.png)
例えば、![]() を積分すると
を積分すると![]() となります。この際、
となります。この際、![]() を微分したものが
を微分したものが![]() となる関係から考えることもできます。また、
となる関係から考えることもできます。また、![]() を0から3まで積分すると次のようになります。
を0から3まで積分すると次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \int_{0}^{3} x^2 dx=\left[ \frac{1}{3}x^3 \right]_{0}^{3} =\left(\frac{1}{3} \times 3^3 \right) - \left(\frac{1}{3} \times 0^3\right) = 9](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-10b17713dc43c860166ba233c71821f2_l3.png)
■kxnの積分公式
![]() のように、ある関数
のように、ある関数![]() を定数倍した関数の積分は次のように計算できます。
を定数倍した関数の積分は次のように計算できます。
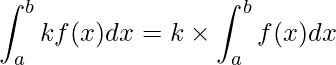
この2つの公式を利用すると、2つの関数![]() と
と![]() の和からなる関数
の和からなる関数![]() の積分は、次のように計算できます。
の積分は、次のように計算できます。
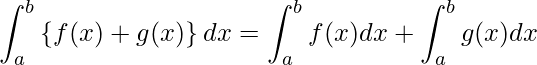
例えば![]() の関数の積分計算は、
の関数の積分計算は、![]() の項と
の項と![]() の項をそれぞれ積分したものを足し合わせたものと等しくなります。この関数を1から3まで積分すると次のようになります。
の項をそれぞれ積分したものを足し合わせたものと等しくなります。この関数を1から3まで積分すると次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \int_{1}^{3} \left\{ x^2 +x \right\} dx=\displaystyle \int_{1}^{3} x^2 dx +\displaystyle \int_{1}^{3} x dx = \left[ \frac{1}{3} x^3 \right]_{1}^{3}+ \left[ \frac{1}{2} x^2 \right]_{1}^{3} \\ = \left( \frac{3^3}{3} - \frac{1^3}{3} \right) + \left( \frac{3^2}{2} - \frac{1^2}{2} \right) = \frac{38}{3}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-1efdea26daa69b8988c179f28ec1a20a_l3.png)
【例題】
次の3つの積分を計算してみましょう。
1.
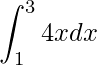
2.
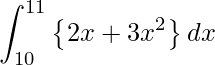
3.
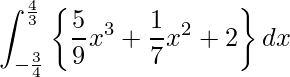
【こたえ】
1.
![Rendered by QuickLaTeX.com \displaystyle \int_{1}^{3} 4x dx = \left[ 2x^2 \right]_{1}^{3}=18-2=16](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-1fb5ff236123bc1d47b4cd634ef8bd7a_l3.png)
2.
![Rendered by QuickLaTeX.com \displaystyle \int_{10}^{11} \left\{ 2x+3x^2 \right\} dx = \left[ x^2 + x^3 \right]_{10}^{11} = (121+1331) - (100+1000) = 352](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-4479eb82056d39d9f1b89113d6edef75_l3.png)
3.
![Rendered by QuickLaTeX.com \displaystyle \int_{-\frac{3}{4}}^{\frac{4}{3}} \left\{ \frac{5}{9}x^3 - \frac{1}{7} x^2 + 2 \right\} dx = \left[\frac{5x^4}{36} - \frac{x^3}{21} + 2x \right]_{-\frac{3}{4}}^{\frac{4}{3}} = \frac{23142125}{5225472}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-97925c3f4da88d3017cb1f3bee522ebb_l3.png)






