数学ノート
統計学で使う数学

指数と累乗根

■指数とは

$a$ を $n$ 回かけたものを $a^n$ と表します。このように、同じ数をかけ合わせたものを「累乗」といいます。また、 $n$ を「指数」といいます。

指数が0の場合、

$\displaystyle a^0 = 1$

となります。また指数が負の数の場合は、

$\displaystyle a^{-n} = \frac{1}{a^n}$

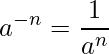
となります。

■指数法則

指数には次に示す「指数法則」が成り立ちます。

$\displaystyle 1.~~~a^m a^n = a^{m+n}$

例えば $a^3 a^4$ について考えてみます。

$\displaystyle a^3 a^4 = (a \times a \times a) \times (a \times a \times a \times a) = a^7 = a^{3+4}$

となることが分かります。また、 $a^4 a^{-2}$ について考えてみます。

$\displaystyle a^4 a^{-2} = \frac{a^4}{a^2} = \frac{a \times a \times a \times a}{a \times a} = a^{2} = a^{4-2}$

となります。

$\displaystyle 2.~~~(a^m)^n = a^{mn}$

例えば $(a^3)^2$ について考えてみます。

$\displaystyle (a^3)^2 = (a \times a \times a)^2 = (a \times a \times a) \times (a \times a \times a) = a^6 = a^{3 \times 2}$

となることが分かります。

$\displaystyle 3.~~~(ab)^n = a^{n}b^{n}$

例えば $(ab)^3$ について考えてみます。

$\displaystyle (ab)^3 = (ab \times ab \times ab) = a \times a \times a \times b \times b \times b = a^3 b^3$

となることが分かります。また、 $\displaystyle \left(\frac{a}{b}\right)^3$ について考えてみます。

$\displaystyle \left(\frac{a}{b}\right)^3 = \left(\frac{a}{b}\right) \times \left(\frac{a}{b}\right) \times \left(\frac{a}{b}\right) = \frac{a \times a \times a}{b \times b \times b} = a^3 \times \left( \frac{1}{b^3} \right) = \frac{a^3}{b^3}$

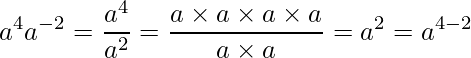
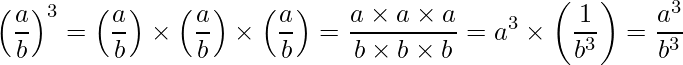
となります。

■累乗根とは

$n$ 乗すると $a$ になる数を $a$ の $n$ 乗根といい、 $\sqrt[n]{a}$ と書きます。特に、2乗すると $a$ になる数を $a$ の平方根（2乗根）、3乗すると $a$ になる数を $a$ の立方根（3乗根）といいます。これらの「○乗根」をまとめて「累乗根」といいます。

$a = 0$ の場合、

$\displaystyle \sqrt[n]{0} = 0$

となります。また、累乗根は次のように書き換えることもできます。

$\displaystyle \sqrt[n]{a} = a^{\frac{1}{n}}$

例えば、3乗すると $a$ になる数 $\sqrt[3]{a}$ について考えてみます。 $\sqrt[3]{a}$ を3乗すると

$\displaystyle (\sqrt[3]{a})^3 = (a^{\frac{1}{3}})^3 = a^{\frac{1}{3} \times 3} = a^1 = a$

となることから、 $\sqrt[n]{a} = a^{\frac{1}{n}}$ が成り立つことが確認できます。

■累乗根の公式

$a>0$ 、 $b>0$ であり、 $m$ 、 $n$ 、 $p$ が正の数のとき、累乗根には次に示す「累乗根の公式」が成り立ちます。

$\displaystyle 1.~~~ \sqrt[n]{a} \sqrt[n]{b} = \sqrt[n]{ab}$

【証明】右辺を $x$ とおきます。

$\displaystyle \sqrt[n]{a} \sqrt[n]{b} = x$

両辺を $n$ 乗すると、

$\displaystyle (\sqrt[n]{a} \sqrt[n]{b})^n = (\sqrt[n]{a})^n (\sqrt[n]{b})^n = (a^{\frac{1}{n}})^n (b^{\frac{1}{n}})^n = (a^{\frac{1}{n} \times n}) (b^{\frac{1}{n} \times n}) = ab = x^n$

となります。 $ab>0$ 、 $x>0$ であることから

$\displaystyle x = \sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b}$

となります。

$\displaystyle 2.~~~\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}$

【証明】右辺を $x$ とおきます。

$\displaystyle \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = x$

両辺を $n$ 乗すると、

$\displaystyle \left(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\right)^n = \frac{(\sqrt[n]{a})^n}{(\sqrt[n]{b})^n} = \frac{(a^{\frac{1}{n}})^n}{(b^{\frac{1}{n}})^n} = \frac{a^{\frac{1}{n} \times n}}{b^{\frac{1}{n} \times n}} = \frac{a}{b} = x^n$

となります。 $\frac{a}{b}>0$ 、 $x>0$ であることから

$\displaystyle x = \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

となります。

$\displaystyle 3.~~~(\sqrt[n]{a})^m = \sqrt[n]{a^m}$

【証明】右辺を $x$ とおきます。

$\displaystyle (\sqrt[n]{a})^m = x$

両辺を $n$ 乗すると、

$\displaystyle ((\sqrt[n]{a})^m)^n = ((a^{\frac{1}{n}})^m)^n = (a^{\frac{1}{n} \times m})^n = (a^{\frac{m}{n}})^n = a^{\frac{m}{n} \times n} = a^m = x^n$

となります。 $a^m>0$ 、 $x>0$ であることから

$\displaystyle x = \sqrt[n]{a^m} = (\sqrt[n]{a})^m$

となります。

$\displaystyle 4.~~~\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}$

【証明】右辺を $x$ とおきます。

$\displaystyle \sqrt[m]{\sqrt[n]{a}} = x$

両辺を $m$ 乗すると、

$\displaystyle \left(\sqrt[m]{\sqrt[n]{a}}\right)^m = ((\sqrt[n]{a})^{\frac{1}{m}})^m = (\sqrt[n]{a})^{\frac{1}{m}\times m} = \sqrt[n]{a} = x^m$

となります。さらに両辺を $n$ 乗すると、

$\displaystyle (\sqrt[n]{a})^n = (a^{\frac{1}{n}})^n = a^{\frac{1}{n} \times n} = a = x^{mn}$

$a>0$ 、 $x>0$ であることから

$\displaystyle x = \sqrt[mn]{a} = \sqrt[m]{\sqrt[n]{a}}$

となります。

$\displaystyle 5.~~~\sqrt[n]{a^m} = \sqrt[np]{a^{mp}}$

【証明】右辺を $x$ とおきます。

$\displaystyle \sqrt[n]{a^m} = x$

両辺を $n$ 乗すると、

$\displaystyle (\sqrt[n]{a^m})^n = (({a^m})^{\frac{1}{n}})^n = ({a^m})^{\frac{1}{n} \times n} = a^m = x^n$

となります。さらに両辺を $p$ 乗します。

$\displaystyle a^{mp} = x^{np}$

$a^{mp}>0$ 、 $x>0$ であることから

$\displaystyle x = \sqrt[np]{a^{mp}} = \sqrt[n]{a^m}$

となります。

【例題】

次の計算式を簡単にするとどうなるでしょうか。

$\displaystyle a^6 \times a^{-2} \times (a^{-3})^2$
$\displaystyle 0.25^{\frac{3}{2}}$
$\displaystyle (16^{\frac{5}{4}} \times 9^{\frac{3}{2}})^3 \div 12^4$
$\displaystyle (m^2 n)^{-2} \times m^{-1}n^3 \div (m^{-3}n^{-1})^2$
$\displaystyle \sqrt{2} \times \sqrt[3]{2} \times \sqrt[4]{2}$
$\displaystyle (x^{\frac{1}{2}} - x^{\frac{1}{2}})(x^{\frac{1}{2}} + x^{\frac{1}{2}})$