- 数学ノート
- 統計学で使う数学
積分とは
積分とは微分と対を成すもので、ある関数から得られる領域の面積を求めることです。積分では「![]() (インテグラル)」という記号を使います。例えば次の式は、「
(インテグラル)」という記号を使います。例えば次の式は、「![]() という関数を
という関数を![]() から
から![]() まで積分する」ということを表します。
まで積分する」ということを表します。
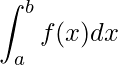
これは、![]() 、
、![]() 、
、![]() 、
、![]() 軸(
軸(![]() )の4本の線で囲まれる部分の面積(次の図の網掛け部分)を計算することを意味します。
)の4本の線で囲まれる部分の面積(次の図の網掛け部分)を計算することを意味します。
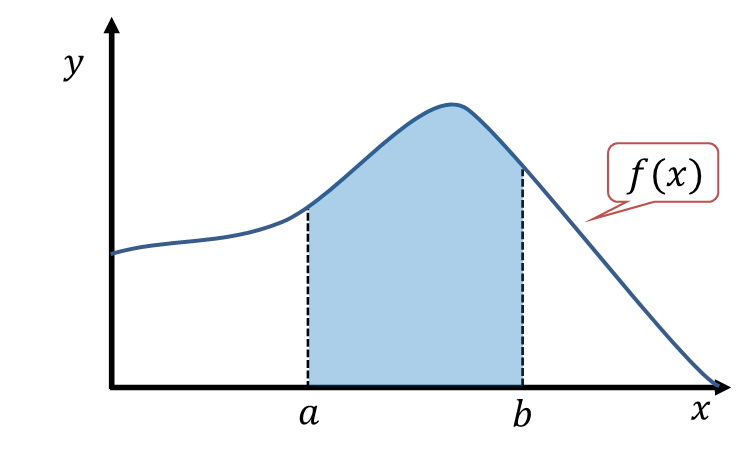
この![]() 関数を使って、積分の考え方を説明します。
関数を使って、積分の考え方を説明します。
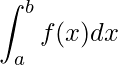
積分の式中の「![]() 」は、非常に小さな長さを表しています。また、「
」は、非常に小さな長さを表しています。また、「![]() 」は、
」は、![]() と
と![]() の積を表しています。
の積を表しています。![]() はある点
はある点![]() における
における![]() の値であることから、
の値であることから、![]() は、下図に示すように「
は、下図に示すように「![]() 」から「
」から「![]() 」までの幅
」までの幅![]() をもつ区間の長方形の面積を表します。
をもつ区間の長方形の面積を表します。
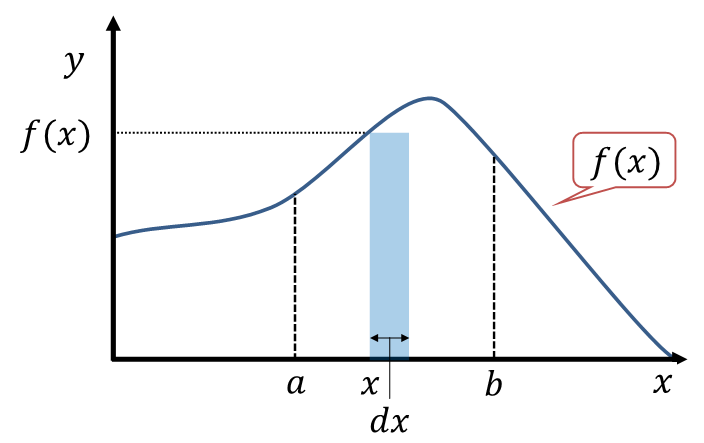
「![]() 」は、前述のようにして作った長方形を
」は、前述のようにして作った長方形を![]() から
から![]() の区間の間まで作り、全て足し合わせるイメージです。
の区間の間まで作り、全て足し合わせるイメージです。
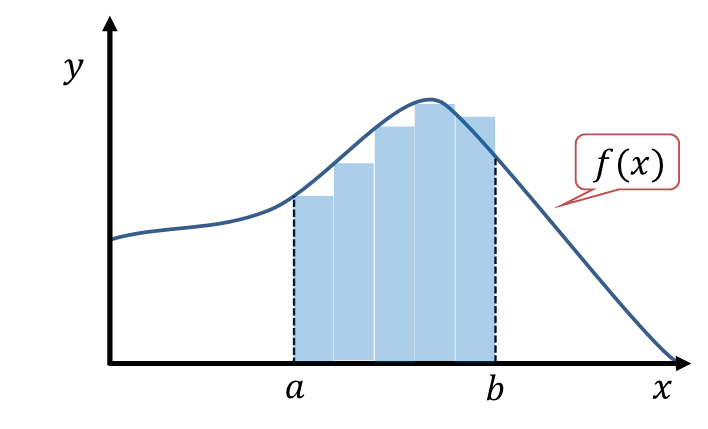
![]() とすると、5個分の長方形の面積を足し合わせることになります。長方形によって
とすると、5個分の長方形の面積を足し合わせることになります。長方形によって![]() の下を覆いきれていない部分や、逆に
の下を覆いきれていない部分や、逆に![]() からはみ出している部分があります。
からはみ出している部分があります。![]() (10個分の長方形)、
(10個分の長方形)、![]() (20個分の長方形)にしたものが次の図です。
(20個分の長方形)にしたものが次の図です。
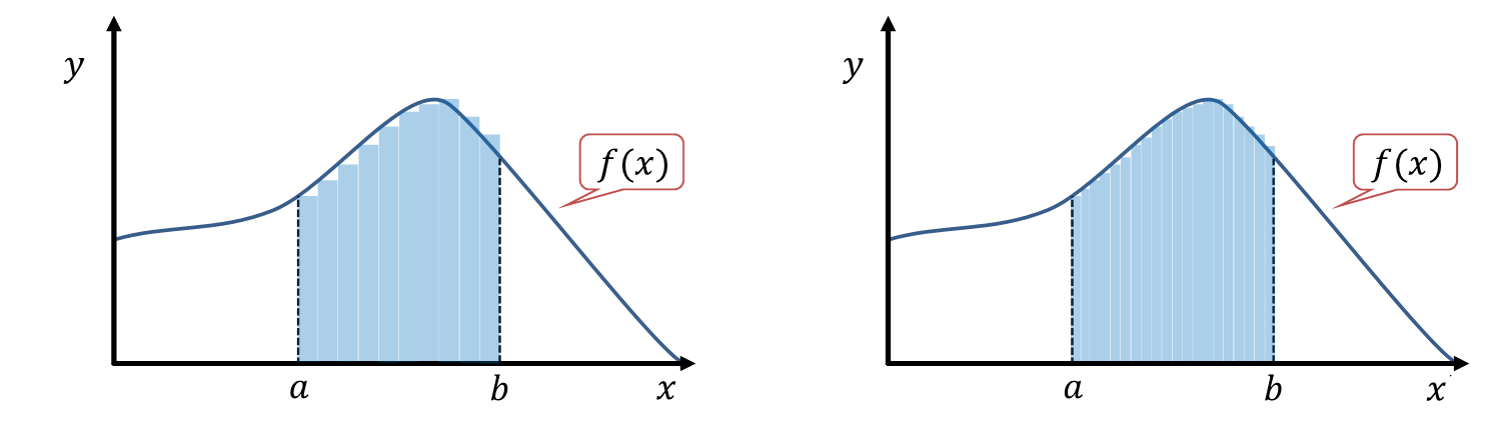
長方形の数を増やしていくことで、覆いきれていない部分やはみ出している部分が段々と小さくなっていきます。このように分割をとても細かくしていき、![]() が非常に小さくなると、最終的には曲線の下の部分の面積に等しくなります。この非常に幅の狭い長方形を
が非常に小さくなると、最終的には曲線の下の部分の面積に等しくなります。この非常に幅の狭い長方形を![]() から
から![]() まで作り、その面積を足し合わせていくことが、積分の考え方です。
まで作り、その面積を足し合わせていくことが、積分の考え方です。
このようにして計算した部分の面積は、最初に述べた通り、![]() 、
、![]() 、
、![]() 、
、![]() で囲まれる部分の面積となります。
で囲まれる部分の面積となります。








