- Step1. 基礎編
- 26. 相関分析
26-3. 相関係数
直線的な相関関係の強さを表す指標の一つに「相関係数(ピアソンの積率相関係数)」があります。2つの要素xとyからなるn個のデータ(![]() ,
, ![]() : i=1, 2,…, n)が得られたとき、その相関係数
: i=1, 2,…, n)が得られたとき、その相関係数![]() は次の式から算出されます。
は次の式から算出されます。
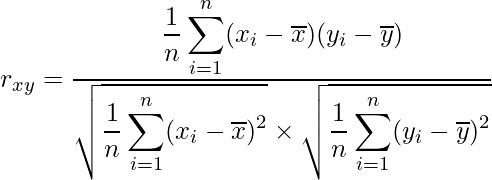
この式の分母はx、yそれぞれの標準偏差の積になっています。また、分子はxとyの「共分散」です。
共分散は、xとyそれぞれの平均値に対する、xとyのペアの値の散らばり方を表すものです。例えば、![]() と
と![]() が共に正もしくは負である場合、
が共に正もしくは負である場合、![]() となります。一方、
となります。一方、![]() と
と![]() が正と負もしくは負と正である場合、
が正と負もしくは負と正である場合、![]() となります。この
となります。この![]() の平均値が共分散なので、共分散が正→xとyのペアの値が共に正もしくは負→相関係数が正の値となります。
の平均値が共分散なので、共分散が正→xとyのペアの値が共に正もしくは負→相関係数が正の値となります。
相関係数rには次のような特徴があります。
- rは-1から1までのいずれかの値をとる
- |r|が1に近いほど相関が強く、0に近いほど相関が弱い
- |r|が0に近くても、何らかの関係がある場合がある
- rは単位を持たない値であり、データの単位がどのようなものであっても計算できる
いくつかの散布図とその相関係数を見てみます。相関係数は上から順に「-0.88」「0.50」「-0.30」です。



次の散布図では相関係数は0.16とあまり高くありませんが、プロットを見てみると放物線を描いておりyはxの二次関数で表すことができそうです。

相関係数は2つの要素の直線的な相関関係の強弱を表すものであり、線形ではない相関関係の強弱は正しく表すことができません。したがって、相関係数rが0に近い場合でも、いきなり「相関なし/相関が弱い」と判断せずにまずはプロットしたグラフを確認してみてください。xとyの間に何らかの関係がある場合に目視で捉えることができます。
■無相関の検定
標本から算出した相関係数を使って、母集団の相関係数が0かどうかを検定することを無相関の検定といいます。標本では相関がある場合に、母集団でも同様に相関があるかどうかを確認できます。帰無仮説は「母相関係数は0(無相関)である」です。
無相関の検定はt分布を用いて行います。次の式から算出される統計量tは自由度n-2のt分布に従います。rは標本から算出した相関係数、nはサンプルサイズを表します。
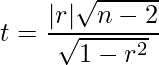
帰無仮説![]() が棄却された場合、「母相関係数は0ではない」すなわち、「2つの要素間で相関関係がある」と結論付けられます。
が棄却された場合、「母相関係数は0ではない」すなわち、「2つの要素間で相関関係がある」と結論付けられます。
■母相関係数の信頼区間
母相関係数の信頼区間を求めるためには、まず次の式を用いて標本から算出した相関係数rを変換します。この変換を「フィッシャーのz変換」といいます。
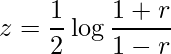
同様に、母相関係数![]() をz変換したものを
をz変換したものを![]() とします。
とします。
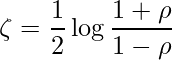
zはサンプルサイズnが大きい時には、平均![]() 、分散
、分散![]() の正規分布
の正規分布![]() に従います。これらを用いてzを標準化すると次のようになります。
に従います。これらを用いてzを標準化すると次のようになります。
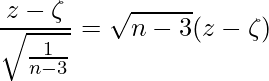
この値が標準正規分布N(0,1)に従うことから、![]() 信頼区間は次のようになります。ただし、
信頼区間は次のようになります。ただし、![]() は標準正規分布における上側確率が
は標準正規分布における上側確率が![]() となる値(z値)を表します。
となる値(z値)を表します。
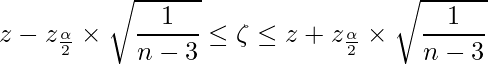
最後に、![]() を母相関係数
を母相関係数![]() に戻します。
に戻します。![]() と
と![]() を次のように置くと、
を次のように置くと、
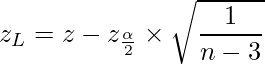
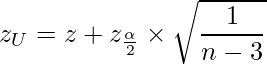
母相関係数![]() の信頼区間は次のようになります。
の信頼区間は次のようになります。
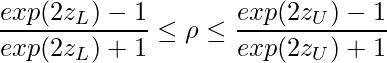
■おすすめ書籍
統計検定®2級の出題範囲には「散布図」、「共分散」、「相関係数」が含まれます。
26. 相関分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- ブログ
共分散は「n」で割る?「n-1」で割る?
- ブログ
幾つデータが必要か? - 相関係数の有意性検定
- ブログ
相関係数を視覚化する
- ブログ
外れ値と相関係数
- ブログ
平均への回帰、相関係数
- ブログ
無相関の検定 - 相関係数の有意性を検定する










