- Step1. 基礎編
- 21. 母比率の区間推定
21-4. 必要なサンプルサイズ1
母比率![]() の95%信頼区間は次の式から求められることは21-1章で既に学びました。
の95%信頼区間は次の式から求められることは21-1章で既に学びました。
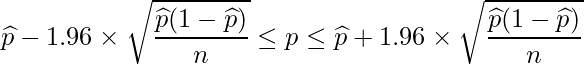
母比率![]() の95%信頼区間は、標本比率
の95%信頼区間は、標本比率![]() の両側に
の両側に![]() ずつ幅を取ったものであると考えることができます。つまり、95%信頼区間の幅は次のようになります。この式を使うと、必要なサンプルサイズを算出できます。
ずつ幅を取ったものであると考えることができます。つまり、95%信頼区間の幅は次のようになります。この式を使うと、必要なサンプルサイズを算出できます。

例題:
テレビ番組の視聴に関する街頭アンケートを行います。信頼係数を95%とし、A番組の視聴率の信頼区間の幅を5%以下にするためには、何人以上の人にアンケートを行わなくてはならないでしょうか。ただし、A番組の視聴率は事前調査により10%以下であることが分かっているものとします。
A番組の視聴率の推定値![]() =0.1を①の式に代入し、nを求めます。①式が5%(=0.05)以下であればいいので、次の関係が成り立ちます。
=0.1を①の式に代入し、nを求めます。①式が5%(=0.05)以下であればいいので、次の関係が成り立ちます。
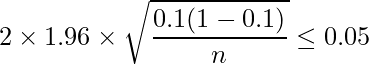
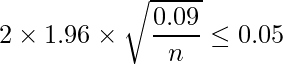
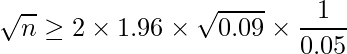
したがって、554人以上の人に対してアンケートを行えばよいという結果になりました。①の式を一般化して信頼係数![]() (=100
(=100![]() %)の場合には、正規分布の累積確率を用いて次のように表せます。
%)の場合には、正規分布の累積確率を用いて次のように表せます。
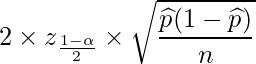
この式から、母比率の信頼区間について次の3点が成り立つことが分かります。
- nが大きくなると信頼区間の幅は狭くなり、より正確な推定ができる
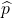 が0.5のとき、最も信頼区間が広くなり、0.5から外れるごとに信頼区間は狭くなる
が0.5のとき、最も信頼区間が広くなり、0.5から外れるごとに信頼区間は狭くなる- 信頼区間の幅は
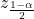 に比例する
に比例する
信頼区間の長さが![]() に反比例しているためです。例えば、nが4倍になると信頼区間の幅は半分になります。
に反比例しているためです。例えば、nが4倍になると信頼区間の幅は半分になります。
![]() の部分が、
の部分が、![]() =0.5のとき最大値を取るためです。
=0.5のとき最大値を取るためです。
※ただし、「信頼区間の幅が±x%以下となるために必要なサンプルサイズ」もしくは「標本誤差をx%以内にするために必要なサンプルサイズ」を求める場合には、
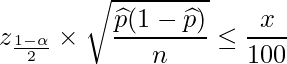
という式を立てて計算する必要があります(「2×」の部分は不要)。
■Tips 母比率の区間推定における必要なサンプルサイズの計算フォーム
こちらのページでは、母比率の区間推定における必要サンプルサイズを自動で計算できます。上で挙げた例題の場合、「誤差:2.5%(標本比率が母比率に対して上下2.5%の範囲内に収まって欲しい=信頼区間を5%以内にする)」、「信頼度:95%」、「母比率:10%」を入力することで、必要サンプルサイズ「554」が算出されます。
![]() の値は信頼係数が高くなるほど大きくなるので、例えば95%信頼区間よりも99%信頼区間の方が信頼区間の幅が広くなります。
の値は信頼係数が高くなるほど大きくなるので、例えば95%信頼区間よりも99%信頼区間の方が信頼区間の幅が広くなります。
■おすすめ書籍
サンプルサイズの計算について網羅的に書かれた(おそらく)唯一の本です。が、結構難しいです…。
21. 母比率の区間推定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
母比率の区間推定(無限母集団)
- 21. 母比率の区間推定
21-1. 母比率の信頼区間の求め方1
- ブログ
sample, population, universe
- ブログ
幾つデータが必要か?







