- Step1. 基礎編
- 3. さまざまな代表値
3-1. 平均・中央値・モード
数値からなるデータがある場合に、そのデータを端的に表す値のことを「代表値」といいます。代表値として使われる値には以下のようなものがあります。
1. 平均
平均は、全てのデータの値![]() を足してデータの数(n)で割ったものです。式で表すと次のようになります。「
を足してデータの数(n)で割ったものです。式で表すと次のようになります。「![]() 」は「エックスバー」と読み、データ
」は「エックスバー」と読み、データ![]() の平均であることを示します。
の平均であることを示します。
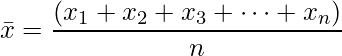
もしデータが度数分布表の形になっている場合は、「階級値」と「度数」を使っておよその平均を算出できます。n個の階級を持つ度数分布表の場合、階級値を![]() 、度数を
、度数を![]() (i=1, 2, …, n)とすると次の式になります。
(i=1, 2, …, n)とすると次の式になります。
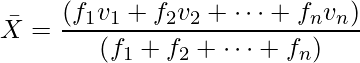
例えば、次に示すあるクラスの生徒の身長の度数分布表について考えてみます。
| 階級 | 階級値 | 度数 |
|---|---|---|
| 140cm以上150cm未満 | 145cm | 2 |
| 150cm以上160cm未満 | 155cm | 5 |
| 160cm以上170cm未満 | 165cm | 7 |
| 170cm以上180cm未満 | 175cm | 3 |
この場合、身長の平均は次のように計算します。
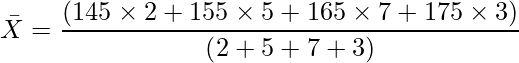
2. 中央値
中央値はメディアン(Median)ともよばれます。データを小さい順に並べたときにちょうど真ん中に来る値のことです。
例えば「1, 1, 2, 4, 5, 8, 9, 10, 11」というデータの場合、中央値は「5」です。もしデータの数が偶数の場合、例えば「1, 1, 2, 4, 5, 8, 9, 10, 11,14」というデータの場合、中央にある2つの値「5」と「8」の平均が中央値となります。したがって、中央値は(5+8)/2=6.5です。
3. モード(最頻値)
モードは最頻値とも呼ばれ、最もデータ数の多い値を指します。例えば「1, 1, 2, 4, 5, 8, 9, 10, 11」というデータの場合、モードは「1」です。
また、度数分布表では最も度数の大きい階級値がモードとなります。次に示すあるクラスの生徒の身長の度数分布表の場合、最も度数の大きい階級は「160cm以上170cm未満」であり、モードはその階級値である165cmとなります。
| 階級 | 階級値 | 度数 |
|---|---|---|
| 140cm以上150cm未満 | 145cm | 2 |
| 150cm以上160cm未満 | 155cm | 5 |
| 160cm以上170cm未満 | 165cm | 7 |
| 170cm以上180cm未満 | 175cm | 3 |
【コラム】モードの数
モードは、データの中で頻度が最も高い値のことですが、データによってはモードが2つある場合があります。例えば「0, 1, 1, 1, 2, 4, 5, 8, 9, 9, 9, 10」というデータの場合、モードは「1」と「9」になります。
一方、「0, 1, 2, 4, 5, 8, 9, 10」というデータの場合、モードはありません。
【コラム】平均はmeanかaverageか
英語には平均値を表す言葉としてaverageとmeanの2つがあります。一般に、averageも mean も特にことわりがなければ「算術平均(Arithmetic mean)」を意味します。
統計学の世界では average と mean を使い分けており、いわゆる平均値には mean を用いるのが常識です。詳しくはこちら
■おすすめ書籍
日本人の、本当にあらゆる項目についての平均が掲載されています!
3. さまざまな代表値
事前に読むと理解が深まる- 学習内容が難しかった方に -
- ブログ
「平均」のこと








