- 4. 箱ひげ図と幹葉表示
練習問題(4. 箱ひげ図と幹葉表示)
1
それぞれ200個ずつのデータからなるデータAとデータBについて箱ひげ図を作成した。この箱ひげ図から読み取った以下5つの記述について、正しいものを答えよ。
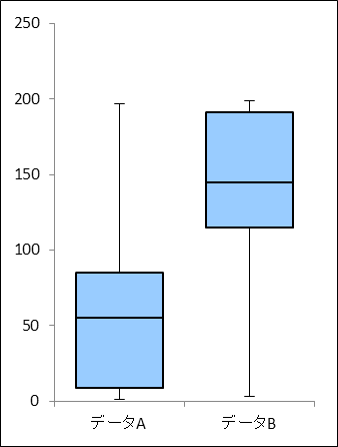
- データAとデータBの最大値は、どちらも同じくらいの値である。
- 箱ひげ図の形状から、データBは左に裾を引く単峰の分布であると言える。
- データAにおいて100以上の値を取るデータ数は、少なくとも50個以上ある。
- データBにおいて100以上の値を取るデータ数は、データAの3倍以上ある。
- データAの中央値とデータBの中央値の差は、およそ100である。

答えを見る
- 答え
 閉じる
閉じる -
- ◯:ひげの上端はどちらも200に近いので、ほぼ同じ程度の値であると考えられます。
- ×:箱ひげ図のみから、峰(=分布の山)の数を読み取ることはできません。
- ×:データAの第三四分位数が100未満であり、データ数が200です。したがって、第三四分位数から最大値までの中におよそ50個のデータがあると考えられます。しかし、第三四分位数から100までの間にデータが存在する可能性もあるので、100以上の値を取るデータ数が必ずしも50個以上あるとは言えません。
- ◯:3.から、データAで100以上の値を取るデータは50個以下です。同様にデータBについて考えると、第一四分位数が100よりも大きい値であることから150個以上のデータが100以上の値を取ります。したがって、データBで100以上となるデータ数はデータAで100以上となるデータ数の3倍以上であると考えられます。
- ◯:データAの中央値は50前後、データBの中央値は150前後であることから、中央値の差はおよそ100であると言えます。
2
次のデータから、四分位範囲(IQR)を求めよ。
「56, 48, 78, 81, 86, 71, 72, 88, 46, 47, 89, 58, 43, 79, 48, 41」

答えを見る
- 答え
 閉じる
閉じる -
- データを小さい順に並べ替えます
- 中央値を求め、上位データと下位データに分けます
- 上位データ:41,43,46,47,48,48,56,58
- 下位データ:71,72,78,79,81,86,88,89
- 中央値:
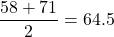
- 上位データと下位データから第一四分位、第三四分位を求めます
- 第一四分位:
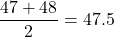
- 第三四分位:
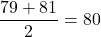
「41, 43, 46, 47, 48, 48, 56, 58, 71, 72, 78, 79, 81, 86, 88, 89」
「41, 43, 46, 47 | 48, 48, 56, 58 | 71, 72, 78, 79 | 81, 86, 88, 89」
以上から、四分位範囲は80-47.5=32.5と計算できます。
3
次のデータから、幹葉表示を作成せよ。
「41, 43.5, 46.9, 56.9, 58.8, 71.4, 78.2, 86.6, 88.5, 89.3」

答えを見る
- 答え
 閉じる
閉じる -
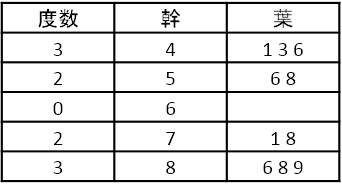
幹葉表示は先頭2桁に注目して作ることが多いため、このデータの場合には小数点は切り捨てて作成します。また、60台のデータが存在しないためこの度数は0となります。
幹葉表示では、「幹」と「葉」とともに「度数」が示されたものがあります。エクセル統計を使うとこのような幹葉表示を出力させることができます。
4
以下の記述のうち、正しいものを選べ。
- 中央値から最小値までの区間と中央値から最大値までの区間が等しい場合、中央値と平均値は等しい。
- データによっては、中央値と第一四分位数が等しくなる場合がある。
- 四分位範囲(IQR)を用いた外れ値検出のある箱ひげ図のひげを描くとき、第三四分位数+1.5×IQRが最大値より大きい場合は最大値をひげの上端とする。
- 幹葉表示だけを見て平均値を求めることができる。
- 幹葉表示を作成するとき、データに対する幹葉表示は必ず1つに定まる。

答えを見る
- 答え
 閉じる
閉じる -
- ×:例えば次のようなデータ「1, 2, 5, 6, 9」の場合、最小値は1、中央値は5、最大値は9であり、中央値-最小値=最大値-中央値=4となりますが、平均値は4.6です。
- ○:例えば次のようなデータ「1, 5, 5, 5, 6, 7, 9」の場合、中央値と第一四分位数はいずれも5です。
- ○:第三四分位数+1.5×IQRが最大値を超える場合、箱ひげ図には観測値が存在する位置をそのまま表示したいので、ひげの上端を最大値として箱ひげ図を作成します。
- ×:問3のように、幹葉表示で表現しきれない部分を切り捨てて幹葉表示が作成されている場合は、幹葉表示だけを見て元データの平均値を求めることはできません。
- ×:幹の区切り方は一定ではありません。例えば次のようなデータ「51, 53, 54, 56, 57, 58, 58, 59, 60, 61, 62」の場合、例1では幹を10刻みで作成していますが、例2では幹を2刻みで作成しています。
【例1】
6 | 0 1 2
5 | 1 3 4 6 7 8 8 9【例2】
6 | 2
6 | 0 1
5 | 8 8 9
5 | 6 7
5 | 4
5 | 3
5 | 1
5
以下の記述のうち、正しいものを選べ。
- 箱ひげ図は高校数学の指導要領に含まれる。
- 横向きの箱ひげ図を描くことはない。
- Excel 2016は、箱ひげ図を作成する機能を搭載している。
- エクセル統計(BellCurve for Excel)の箱ひげ図は、6種類の箱ひげ図を出力することができる。
- エクセル統計(BellCurve for Excel)は、ヒストグラムと箱ひげ図を1つのグラフで出力する機能を搭載している。

答えを見る
- 答え
 閉じる
閉じる -
- ◯:数学1の「データの分析」に箱ひげ図が含まれます。また、数学Bには「確率分布と統計的な推測」という単元もあります。
- ×:縦方向の箱ひげ図をよく見かけますが、必ず縦方向でないといけないということはありません。
- ◯:Excel 2016で箱ひげ図を作成する手順については、「箱ひげ図を作成する - Office のサポート - Office Support」をご確認ください。
- ◯:エクセル統計の分析例ファイルまたはエクセル統計の無料体験版にてご確認ください。
- ◯:エクセル統計の分析例ファイルまたはエクセル統計の無料体験版にてご確認ください。







