- Step1. 基礎編
- 4. 箱ひげ図と幹葉表示
4-4. 箱ひげ図の書き方(データ数が奇数の場合)
例題:
次のような15個のデータから箱ひげ図を作成してみましょう。
「52 , 55 , 65 , 80 , 73 , 63 , 68 , 59 , 60 , 57 , 61 , 77 , 79 , 54 , 110」
箱ひげ図の作成にあたっては、四分位数の情報が必要です。四分位数の求め方にはいくつかの方法がありますが、ここでは高校の学習指導要領に沿った方法を説明します。
- データを小さい順に並べ替え、小さい順に順位をつける
- データの最大値と最小値を求める
- 中央値(第二四分位数)を求める
- 第一四分位数と第三四分位数を計算する
- 箱ひげ図を書く

最大値は「110」、最小値は「52」です。

第二四分位数は中央値と等しいので、中央値を求めます。データの数が奇数のときは、中央値はデータを小さい順に並べたときにちょうど真ん中にある値です。データの数が偶数のときは、真ん中に最も近い2つの値の平均値が中央値となります。このデータはデータ数が15で奇数なので、8番目のデータが中央値となります。したがって中央値は「63」です。

中央値を除いて数値が小さいほうの下位データと数値が大きいほうの上位データに分けたとき、下位データの中央値が第一四分位数、上位データの中央値が第三四分位数となります。上位データ、下位データについても、データ数が奇数であれば順位が真ん中のデータが、偶数の場合には真ん中に最も近い二つのデータの平均値が中央値となります。

このデータでは、7個ずつのデータに分けられます。7は奇数なので、下位データ、上位データのどちらも4番目のデータが中央値となります。したがって、第一四分位数は「57」、第三四分位数は「77」となります。

手順2から手順4までで求めた値を整理すると、次の図のようになります。

この結果から、箱ひげ図を作成します。ひげの上端を「110」、下端を「52」、箱の上端を「77」、下端を「57」、中央値を「63」となるように描くと、箱ひげ図の完成です。
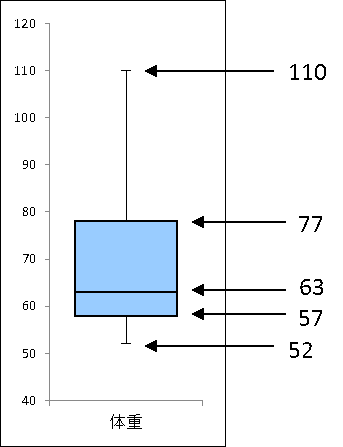
4. 箱ひげ図と幹葉表示
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 4. 箱ひげ図と幹葉表示
4-1. 箱ひげ図とは
- 4. 箱ひげ図と幹葉表示
4-2. 箱ひげ図の見方
- 統計Tips
箱ひげ図の作り方(棒グラフ編)
- 統計Tips
箱ひげ図の作り方(株価チャート編)
- 統計解析事例
記述統計量
- 統計解析事例
箱ひげ図
- ブログ
外れ値の見つけ方







