- Step2. 中級編
- 4. 連続型確率分布
4-2. ガンマ分布
ガンマ分布は連続型確率分布の一つで、指数分布を一般化させることで様々な事象や分野で使われる分布です。例えば、人の体重やウイルスの潜伏期間、電子部品の寿命などはガンマ分布に従うといわれており、これらの数理モデル化においてガンマ分布はよく使われます。ある期間 ![]() ごとに平均して1回起こる現象が、
ごとに平均して1回起こる現象が、![]() 回起きるまでの期間
回起きるまでの期間 ![]() がガンマ分布に従うとき、
がガンマ分布に従うとき、![]() となる確率密度関数
となる確率密度関数 ![]() は次の式で表されます。
は次の式で表されます。![]() と
と![]() はガンマ分布のパラメータであり、それぞれ形状母数、尺度母数とよばれます。
はガンマ分布のパラメータであり、それぞれ形状母数、尺度母数とよばれます。
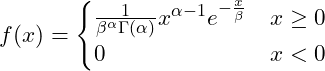
![]() は次に示すガンマ関数を表します。
は次に示すガンマ関数を表します。
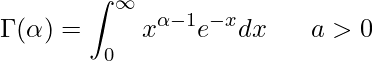
![]() が自然数の場合には次の式が成り立ちます。
が自然数の場合には次の式が成り立ちます。
![]() の場合、
の場合、
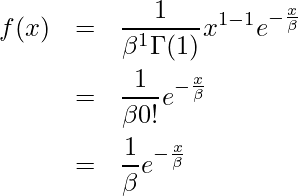
となります。この式は、期待値が ![]() である指数分布の確率密度関数に一致することが分かります。ある期間に平均して
である指数分布の確率密度関数に一致することが分かります。ある期間に平均して ![]() 回起こる現象が、次に起こるまでの期間
回起こる現象が、次に起こるまでの期間 ![]() が従う分布が指数分布です。
が従う分布が指数分布です。
一方ガンマ分布での定義の場合、ある期間![]() ごとに平均して1回起こる現象が、1回起きるまでの期間
ごとに平均して1回起こる現象が、1回起きるまでの期間 ![]() が従う分布がガンマ分布です。これは、「ある期間に平均して
が従う分布がガンマ分布です。これは、「ある期間に平均して ![]() 回起こる現象が、1回起きるまでの期間
回起こる現象が、1回起きるまでの期間 ![]() が従う分布」と書き換えられることから、
が従う分布」と書き換えられることから、![]() の場合のガンマ分布は指数分布に一致することが確認できます。
の場合のガンマ分布は指数分布に一致することが確認できます。
■ガンマ分布の期待値、分散、モーメント母関数
![]() が
が ![]() のガンマ分布に従うとき、
のガンマ分布に従うとき、![]() の期待値
の期待値 ![]() 、分散
、分散 ![]() 、モーメント母関数
、モーメント母関数 ![]() は次のようになります。
は次のようになります。
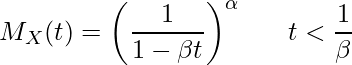
例えば、5分ごとに平均1人が来客するお店において、20人の客が来るまでの時間 ![]() の期待値を求めてみます。この例では
の期待値を求めてみます。この例では ![]() =20、
=20、![]() =5 です。したがって求める期待値は
=5 です。したがって求める期待値は
より、100分(1時間40分)となります。
■ガンマ分布の再生性
ガンマ分布は再生性を持ちます。すなわち、ガンマ分布 ![]() に従うあるデータと、そのデータとは独立なガンマ分布
に従うあるデータと、そのデータとは独立なガンマ分布 ![]() に従うデータを足したデータは、ガンマ分布
に従うデータを足したデータは、ガンマ分布 ![]() に従います。
に従います。







