- Step2. 中級編
- 4. 連続型確率分布
4-1. 正規分布
14-1章で、正規分布に従う確率変数 ![]() の期待値が
の期待値が ![]() 、分散が
、分散が ![]() の場合、確率密度関数
の場合、確率密度関数 ![]() は次の式で表されることを学びました。
は次の式で表されることを学びました。
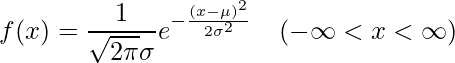
この式から正規分布 ![]() の期待値を求めてみます。
の期待値を求めてみます。
■期待値の算出
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X] &=& \int_{-\infty}^{\infty} x \times f(x) dx \\ &=& \int_{-\infty}^{\infty} x \times \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} x e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} (x - \mu + \mu) e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} (x - \mu) e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx + \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} \mu e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx\\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} (x - \mu) e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx + \mu \times \int_{-\infty}^{\infty} f(x) dx\\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} (x - \mu) e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx + \mu \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-a77b8378d11c62a018227a2f0bbb6bca_l3.png)
ここで、![]() とおくと
とおくと
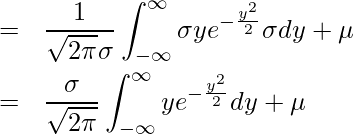
ガウス積分の公式より ![]() となるので、
となるので、
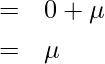
となります。
■分散の算出
分散を求めるには、![]() を使います。まず
を使います。まず![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2] &=& \int_{-\infty}^{\infty} x^2 \times f(x) dx \\ &=& \int_{-\infty}^{\infty} x^2 \times \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} (x^2 - 2x\mu + \mu^2 + 2x\mu -\mu^2) e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \left\{\int_{-\infty}^{\infty} (x - \mu)^2 e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx + 2\mu \int_{-\infty}^{\infty} x e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx - \mu^2 \int_{-\infty}^{\infty} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \right\} \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} (x - \mu)^2 e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx + \frac{2\mu}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} x e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx - \frac{\mu^2}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-62dab8932b1e966a15969d59159f47fc_l3.png)
ここで、![]() なので、
なので、![]() となります。
となります。
また、![]() は正規分布の確率密度関数の積分であることから
は正規分布の確率密度関数の積分であることから ![]() となります。すなわち、
となります。すなわち、![]() となります。
となります。
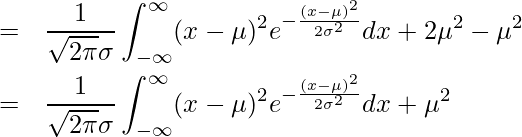
![]() とおくと
とおくと
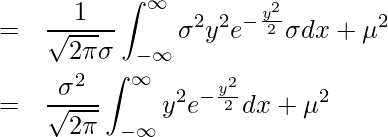
ガウス積分の公式より ![]() となるので、
となるので、
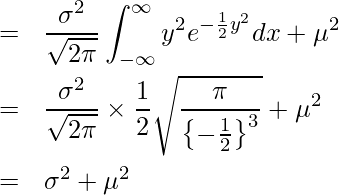
となります。次に![]() を求めます。
を求めます。
これらを使って分散![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& \sigma^2 + \mu^2 - \mu^2 \\ &=& \sigma^2 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-fc25c30ad5591caa56296a1b2020dda5_l3.png)
となります。正規分布の分散の導出については「正規分布の分散を計算する」や「正規分布の分散を計算する の解説」も参考にしてみてください。
■モーメント母関数を用いた期待値の算出
2-1章で学んだモーメント母関数を使って期待値を算出してみます。まずはじめに正規分布のモーメント母関数を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M_X(t) &=& E[e^{tX}] \\ &=& \int_{-\infty}^{\infty}{e^{tx}f(x)} dx \\ &=& \int_{-\infty}^{\infty} e^{tx} \times \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{tx} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}} + tx} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{x^2-2x\mu+\mu^2-2\sigma^2tx}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{x^2-2(\mu+\sigma^2t)x+\mu^2}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{\{x-(\mu+\sigma^2t)\}^2+\mu^2-(\mu+\sigma^2t)^2}{2\sigma^{2}}} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{\{x-(\mu+\sigma^2t)\}^2+\mu^2-\mu^2-2\sigma^2t\mu-\sigma^4t^2} {2\sigma^{2}}} dx\\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{\{x-(\mu+\sigma^2t)\}^2-2\sigma^2t\mu-\sigma^4t^2} {2\sigma^{2}}} dx\\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{\{x-(\mu-\sigma^2t)\}^2}{2\sigma^{2}}} \times e^{\frac{2\sigma^2t\mu}{2\sigma^{2}}} \times e^{\frac{\sigma^4t^2}{2\sigma^{2}}} dx\\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{\{x-(\mu-\sigma^2t)\}^2}{2\sigma^{2}}} \times e^{t\mu} \times e^{\frac{\sigma^2t^2}{2}} dx\\ &=& e^{t\mu+\frac{\sigma^2t^2}{2}} \times \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty} e^{-\frac{\{x-(\mu-\sigma^2t)\}^2}{2\sigma^{2}}} dx\\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7a508ed9e87c4015b61552b7d7f25cfc_l3.png)
![]() は正規分布(平均
は正規分布(平均 ![]() 、分散
、分散 ![]() )の確率密度関数の積分であることから
)の確率密度関数の積分であることから ![]() となります。
となります。
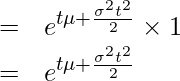
となります。2-1章で学んだように
であることから、まず![]() をtで1回微分します。
をtで1回微分します。
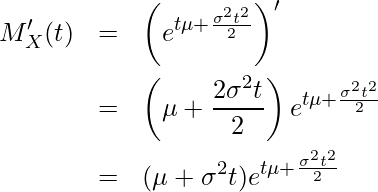
0を代入すると
となります。
■モーメントを用いた分散の算出
2-1章で学んだように
であることから、![]() をtで2回微分します。
をtで2回微分します。
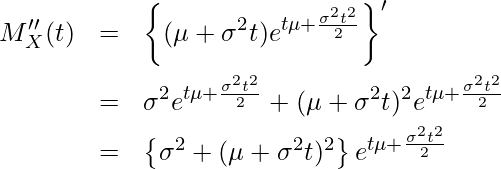
0を代入すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M''_X(0) &=& E[X^2] \\ &=& \left\{\sigma^2 + (\mu + \sigma^2t)^2 \right\} e^{t\mu+\frac{\sigma^2t^2}{2}} \\ &=& \left\{\sigma^2 + (\mu + 0)^2 \right\} \times 1 \\ &=& \sigma^2 + \mu^2 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-26840cbe66fef7aa96f1a0dd3cffeb7b_l3.png)
となることから、V[X]は次のように計算できます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& \sigma^2 + \mu^2 - \mu^2 \\ &=& \sigma^2 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-bf3c520d557347282d2bb5cee51e1c59_l3.png)







