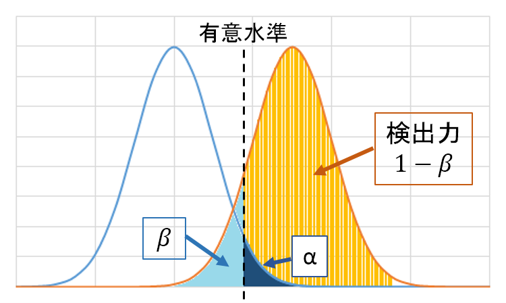
検出力については23-3章で既に学びました。次の図の青色で描かれた曲線を帰無仮説による分布、オレンジ色で描かれた曲線を対立仮説による分布とすると、オレンジ色で塗られた部分が検出力です。

ある薬の効果の検定において、「薬の効果は無い」という帰無仮説を設定したとします。この検定でP値が0.01となった場合、有意水準5%では帰無仮説は棄却されます。しかしP値だけでは「実際に薬の効果がある場合に、きちんと効果があると判断される確率＝帰無仮説が正しくない時（対立仮説が正しい時）に、正しく帰無仮説を棄却する確率（：検出力）」は分かりません。

検出力を算出することで、検定結果の信頼性を知ることができます。もし検出力が小さい場合、本当は差があるのにないと判断される可能性が高いことから、結果を信用することはできなくなります。すなわち、第2種の誤りを犯す可能性が高くなってしまいます。多くの場合、検出力を0.8に設定しますが、これは「80％の確率で、有意差があるときにそれを正しく検出できる」ということを意味します。

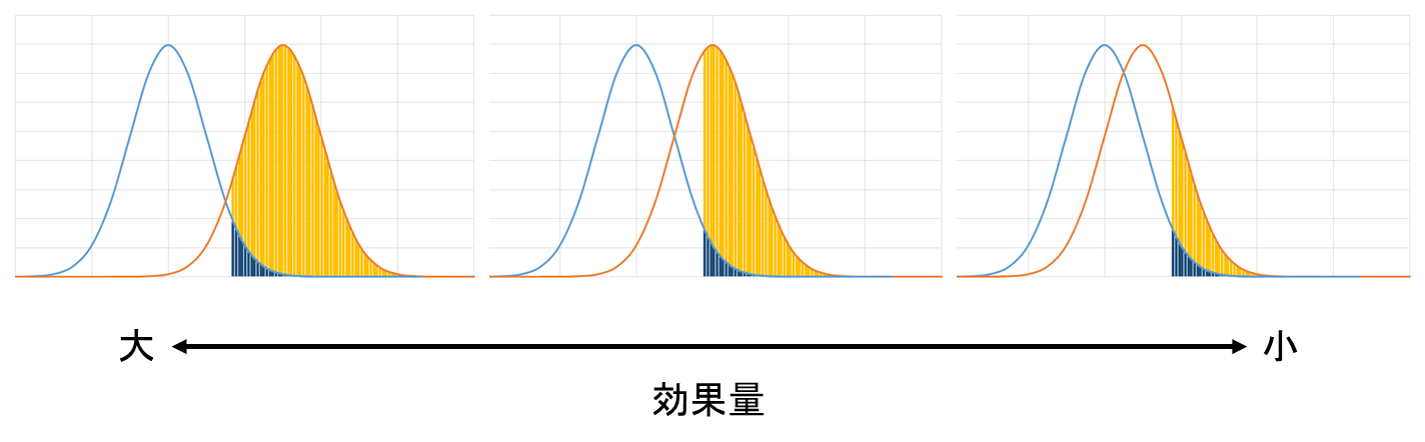
次の図で示すように、検出力は効果量が大きいほど大きくなります。

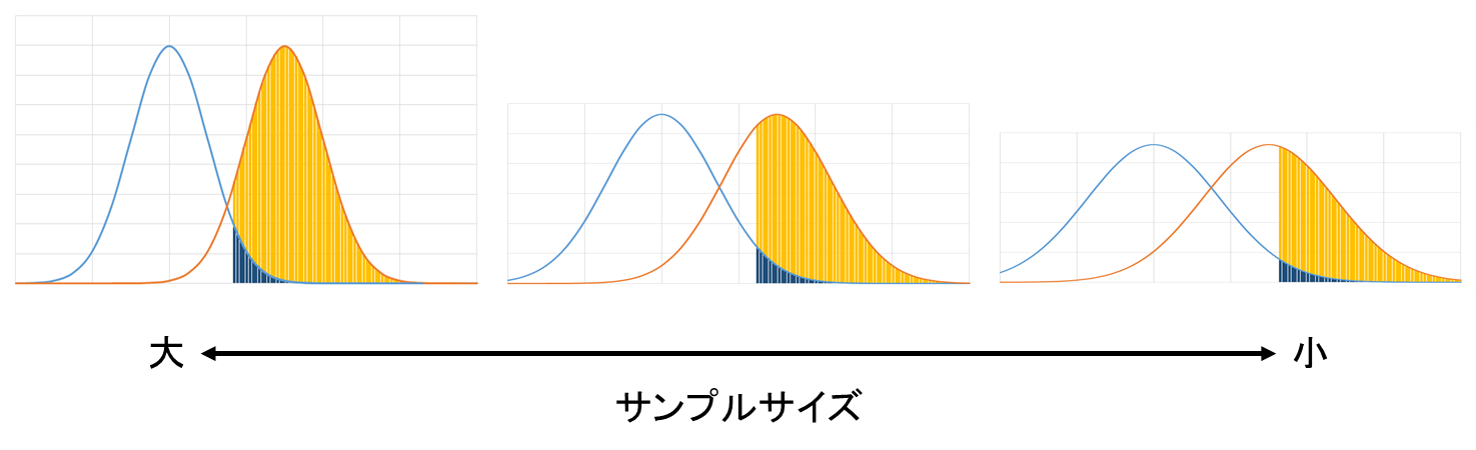
また、17-4章の中心極限定理で学んだようにサンプルサイズが大きいほど分布のばらつきは小さくなるため、検出力は大きくなります。