- Step1. 基礎編
- 31. 実験計画
31-2. 効果量1
「サンプルサイズが大きいほうが母平均をより正確に推測できる」ことは17-2章の大数の法則で既に学びました。しかし、ヒトや動物を対象にした安全性に関する実験や非常にコストの高い実験では、むやみやたらとサンプルサイズを大きくすることはできません。このようなときには「有意水準」、「効果量」、「検出力」を考えた上でサンプルサイズを考えます。
この章ではまず「効果量」について説明します。
効果量は「検出したい差の程度」や「変数間の関係の強さ」のことで、その実験の効果を見るための指標です。P値はその値より極端な値をとる確率を示したものに過ぎないため、その実験において実際にどの程度の効果があったかを知ることはできません。17-4章の中心極限定理で学んだように、サンプルサイズが大きいほうが平均値のばらつきは少ないため、例えば同じ平均値の2群を比較した場合にはサンプルサイズが大きい方がP値は小さくなります。
例題1:
ある学校で、試験対策として20人の生徒に対して補習授業を行いました。この補習授業の効果はあったと言えるでしょうか。
| 補習前(点) | 補習後(点) |
|---|---|
| 97 | 98 |
| 69 | 46 |
| 90 | 78 |
| 65 | 76 |
| 47 | 59 |
| 20 | 32 |
| 89 | 65 |
| 98 | 70 |
| 100 | 100 |
| 83 | 92 |
| 66 | 89 |
| 77 | 71 |
| 29 | 55 |
| 87 | 100 |
| 52 | 67 |
| 50 | 65 |
| 81 | 86 |
| 80 | 79 |
| 60 | 96 |
| 73 | 94 |
補習授業前の平均は70.65点、一方で補習後の平均は75.9点でした。対応のあるt検定(片側検定)を行ってみるとP値は0.0936となり、有意水準を5%とすると帰無仮説![]() 「補習前後の点数は等しい」は棄却されないという結果になります。したがって、補習後の点数は補習前より高いとはいえないと結論付けられます。
「補習前後の点数は等しい」は棄却されないという結果になります。したがって、補習後の点数は補習前より高いとはいえないと結論付けられます。

例題2:
ある学校で、試験対策として40人の生徒に対して補習授業を行いました。この補習授業の効果はあったと言えるでしょうか。
| 補習前(点) | 補習後(点) |
|---|---|
| 97 | 98 |
| 46 | 69 |
| 90 | 78 |
| 65 | 76 |
| 47 | 59 |
| 20 | 32 |
| 89 | 65 |
| 98 | 70 |
| 100 | 100 |
| 83 | 92 |
| 66 | 89 |
| 77 | 71 |
| 29 | 55 |
| 87 | 100 |
| 52 | 67 |
| 50 | 65 |
| 81 | 86 |
| 80 | 79 |
| 60 | 96 |
| 73 | 94 |
| 81 | 86 |
| 32 | 34 |
| 56 | 51 |
| 74 | 97 |
| 85 | 96 |
| 93 | 99 |
| 95 | 97 |
| 52 | 62 |
| 94 | 98 |
| 44 | 41 |
| 78 | 73 |
| 100 | 98 |
| 40 | 41 |
| 68 | 60 |
| 77 | 59 |
| 99 | 99 |
| 65 | 67 |
| 65 | 58 |
| 58 | 93 |
| 80 | 86 |
平均点は先程の例題1と同じです(わざとそういうデータにしているためです)が、P値を見てみると0.0114となりました。5%有意水準の元では帰無仮説![]() 「補習前後の点数は等しい」は棄却されます。したがって、補習後の点数は補習前の点数と比較して高くなったと結論付けられます。
「補習前後の点数は等しい」は棄却されます。したがって、補習後の点数は補習前の点数と比較して高くなったと結論付けられます。
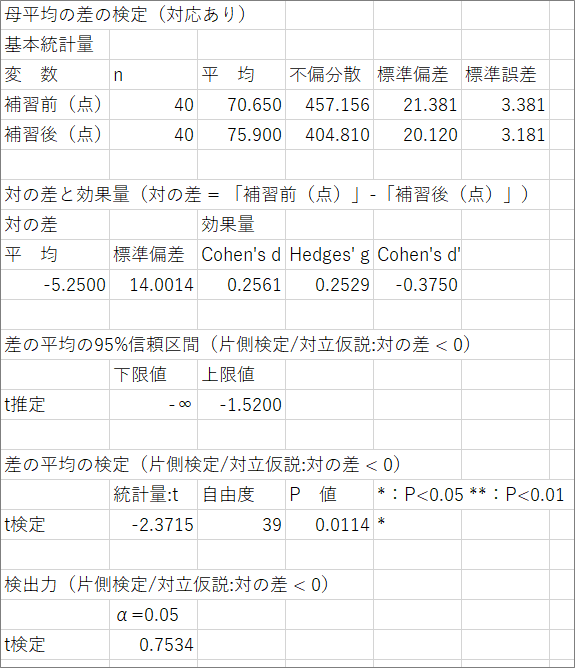
平均値は同じなのに生徒の数が増えたことでP値が小さくなりました。そこで、サンプルサイズによらない効果を示す指標である「効果量」が必要となるわけです。
■おすすめ書籍
APAは「アメリカ心理学会」のことで、この本では論文の執筆基準について書かれています。「データは、読者が基本的な分析をでき、かつ、関心の高い読者が、論文そのもののなかで提示されるデータ以上の、効果量の予測や信頼区間の構築を可能とするものでなければならない。」という記述があり、効果量などの重要性について明示されています。
31. 実験計画
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
母平均の差の検定─エクセル統計による解析事例









