- Step1. 基礎編
- 31. 実験計画
31-3. 効果量2
効果量を表す指標には様々なものがありますが、大きく分けると「d族」と「r族」があります。d族の効果量は差の大きさを表すもので、r族の効果量は相関の強さを表すものです。
d族の効果量には「Cohenのd」と「Hedgesのg」があります。これらは2つの標本間の平均値の差を標準偏差で割って標準化したもので、2標本の平均値の差を比較する際に使います。すなわち、2標本の平均値がどれだけ離れているかを表します。
1群目の標本平均を
、サンプルサイズを
、標本分散を
、不偏分散を
、2群目の標本平均を
、サンプルサイズを
、標本分散を
、不偏分散を
とすると、それぞれの効果量は次の式から算出できます。
■Cohenのd
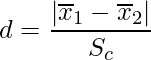
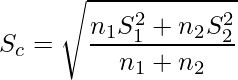
■Hedgesのg
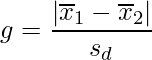
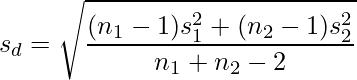
次の図で示すように、これらの効果量の値が大きいほど2つの標本における平均値が離れていることになるので、実験の効果が大きかったと言えます。
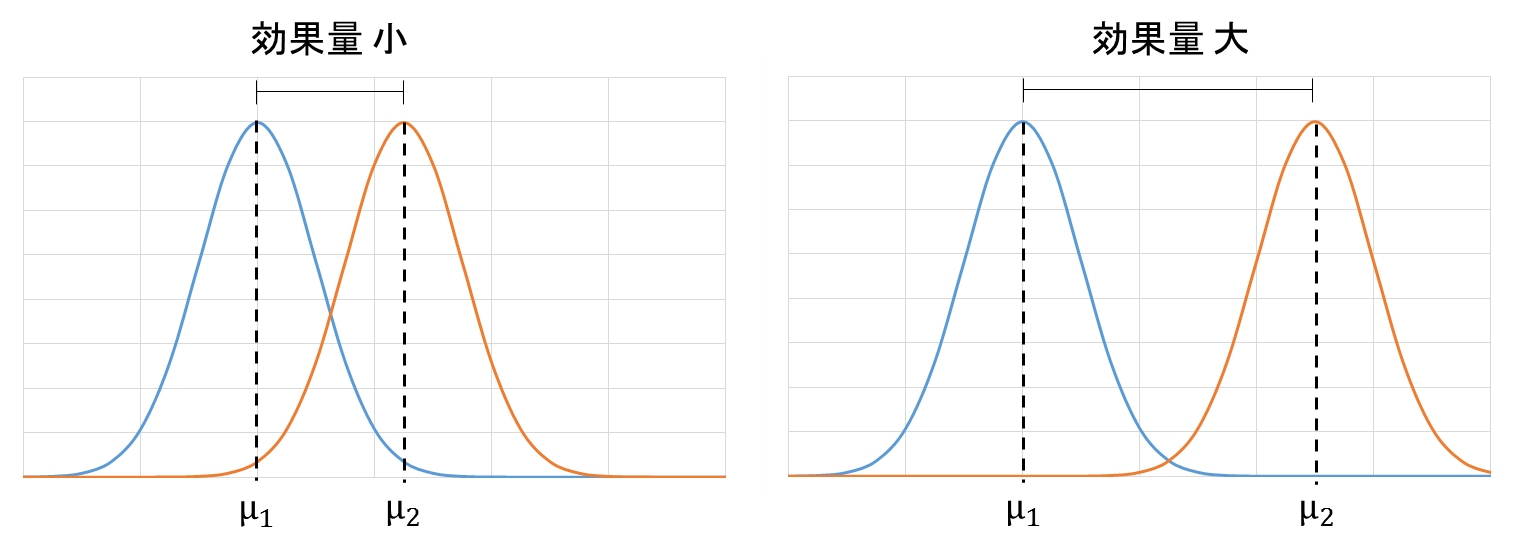
31-2章の例題1と例題2の効果量を比較してみると、ほぼ等しいという結果でした。すなわち2つの標本の平均値の離れ方の程度は同じであると言えます。
| 20人に対する補習授業 | 40人に対する補習授業 | |
|---|---|---|
| サンプルサイズ | 20 | 40 |
| 平均値の差 | 5.25 | 5.25 |
| P値 | 0.0936 | 0.0286 |
| 効果量（Cohenのd） | 0.2599 | 0.2561 |
| 効果量（Hedgesのg） | 0.2533 | 0.2529 |
■おすすめ書籍
近年、P値を算出したときに、その実験にどのくらいの効果があったのかを示す上で、P値とともに効果量を報告することが推奨されています（APA Publication manual）。この章では効果量について簡単にしか触れていませんが、もっと詳しく学びたい方はこちらの書籍をご覧ください。
31. 実験計画
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
母平均の差の検定─エクセル統計による解析事例
