- Step1. 基礎編
- 31. 実験計画
31-5. 検出力の計算
■例題1:
母分散が![]() の正規分布に従う母集団から標本を抽出し、帰無仮説
の正規分布に従う母集団から標本を抽出し、帰無仮説 ![]() 、対立仮説
、対立仮説 ![]() という条件で片側検定を行います。有意水準を5%とするとき、抽出したサンプルサイズが
という条件で片側検定を行います。有意水準を5%とするとき、抽出したサンプルサイズが ![]() の場合の検出力はそれぞれいくらになるでしょうか。
の場合の検出力はそれぞれいくらになるでしょうか。
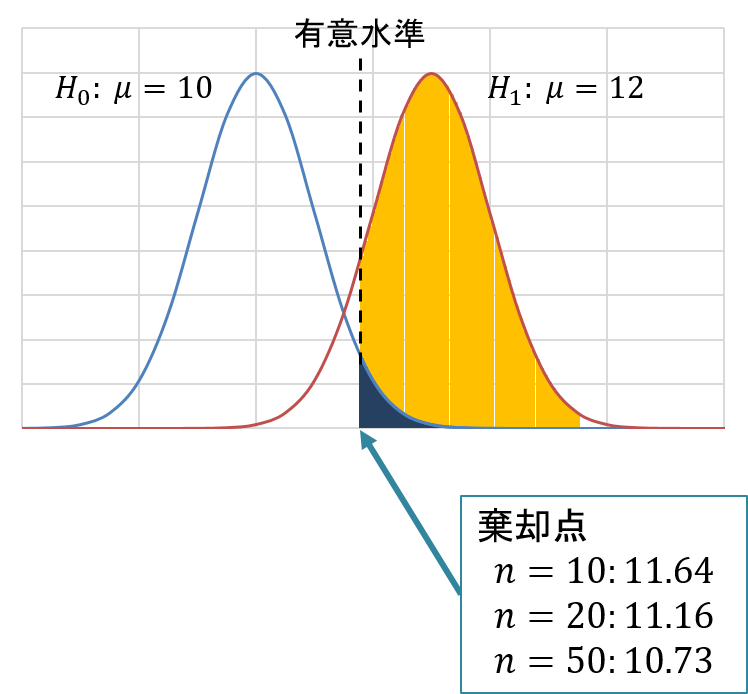
まず、帰無仮説 ![]() が正しいと仮定した場合の棄却点を求めます。
が正しいと仮定した場合の棄却点を求めます。
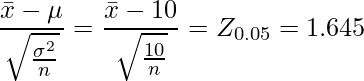
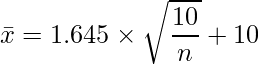
となることから、![]() の場合は
の場合は ![]() 、
、![]() の場合は
の場合は ![]() 、
、![]() の場合は
の場合は ![]() となります。
となります。
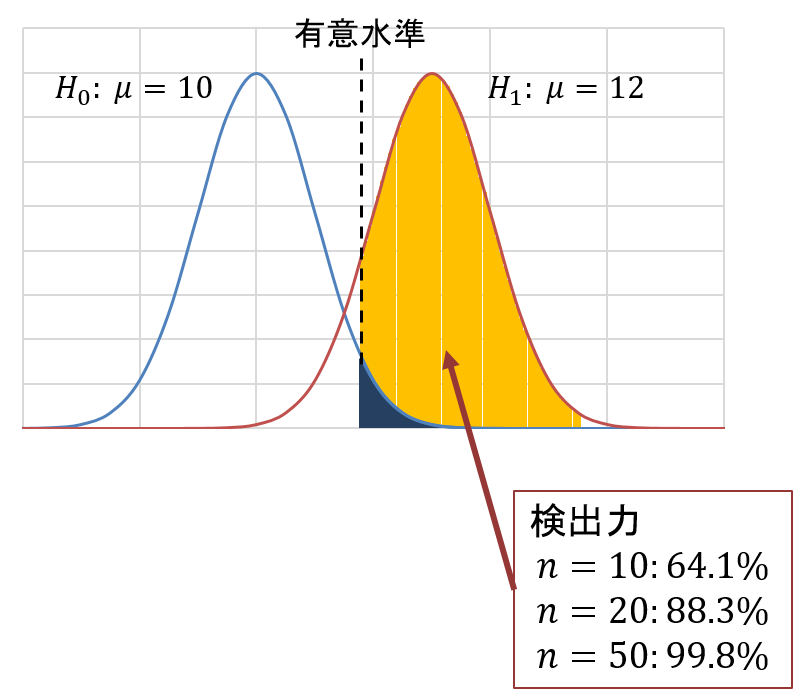
次に、対立仮説 ![]() が正しいと仮定した場合に、この棄却点以上の値を取る確率(=検出力)を求めます。標準正規分布に従う確率変数を
が正しいと仮定した場合に、この棄却点以上の値を取る確率(=検出力)を求めます。標準正規分布に従う確率変数を ![]() とします。
とします。![]() の場合、
の場合、
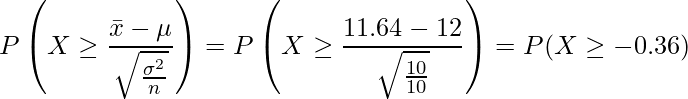
![]() の場合、
の場合、
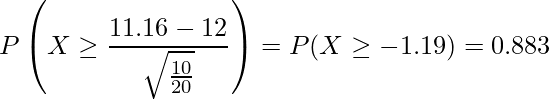
![]() の場合、
の場合、
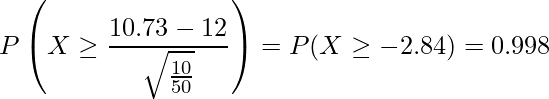
となります。すなわち、検出力はそれぞれ ![]() の場合は
の場合は ![]() 、
、![]() の場合は
の場合は ![]() 、
、![]() の場合は
の場合は ![]() となります。
となります。
このように、サンプルサイズが大きくなるほど検出力は向上します。したがって、実験計画においてはじめに検出力を設定することで、必要なサンプルサイズを計算することができます。
■例題2:
母分散が![]() の正規分布に従う母集団から標本を抽出し、帰無仮説
の正規分布に従う母集団から標本を抽出し、帰無仮説 ![]() 、対立仮説
、対立仮説 ![]() 、
、![]() 、
、![]() という条件で片側検定を行います。有意水準を5%とするとき、抽出したサンプルサイズが
という条件で片側検定を行います。有意水準を5%とするとき、抽出したサンプルサイズが ![]() の場合の検出力はそれぞれいくらになるでしょうか。
の場合の検出力はそれぞれいくらになるでしょうか。
■例題3:
母分散が![]() の正規分布に従う母集団から標本を抽出し、帰無仮説
の正規分布に従う母集団から標本を抽出し、帰無仮説 ![]() 、対立仮説
、対立仮説 ![]() という条件で片側検定を行います。有意水準を10%、5%、1%とするとき、抽出したサンプルサイズが
という条件で片側検定を行います。有意水準を10%、5%、1%とするとき、抽出したサンプルサイズが ![]() の場合の検出力はそれぞれいくらになるでしょうか。
の場合の検出力はそれぞれいくらになるでしょうか。
例題1、2、3の結果をまとめたものが次の表になります。
| 変化させた条件 | 検出力 |
|---|---|
| 例題1:サンプルサイズ | |
| 例題2:平均値の差 | |
| 例題3:有意水準 |
サンプルサイズが大きいほど、効果量が大きいほど、有意水準が大きいほど検出力が向上します。