- Step1. 基礎編
- 25. さまざまな検定
25-5. 独立性の検定
2つ以上の分類基準を持つクロス集計表において、分類基準間に関連があるかどうかを検定することを独立性の検定といいます。このような場合にもカイ二乗分布による検定を使います。
例題:
ランダムに選ばれた男女各100人の血液型について次のようなデータが得られました。この結果から、性別と血液型に関連があるといえるでしょうか。
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 男性 | 55 | 22 | 16 | 7 | 100 |
| 女性 | 40 | 32 | 24 | 4 | 100 |
- 仮説を立てる
- 有意水準を設定する
- 適切な検定統計量を決める
- 棄却ルールを決める
- 検定統計量を元に結論を出す
帰無仮説![]() は「性別と血液型は独立である(関連がない)」とします。したがって、対立仮説
は「性別と血液型は独立である(関連がない)」とします。したがって、対立仮説![]() は「性別と血液型は独立ではない(関連がある)」となります。
は「性別と血液型は独立ではない(関連がある)」となります。
![]() とします。
とします。
適合度検定ではカイ二乗分布に従うカイ二乗統計量(=カイ二乗値![]() )使います。カイ二乗値は次のように求めます。
)使います。カイ二乗値は次のように求めます。
①理論値を算出する
独立性の検定においても適合度の検定と同様に「実測値」を「理論値」と比較します。そのためには「理論値」を算出する必要があります。例えば、「男性・A型」の場合、A型95人が男女1:1に分かれているのが理想なので、
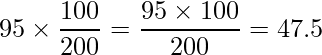
という計算式から「理論値」を算出します。
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 男性 | 55 | 22 | 16 | 7 | 100 |
| 女性 | 40 | 32 | 24 | 4 | 100 |
| 計 | 95 | 54 | 40 | 11 | 200 |
同様にしてすべての「理論値」を算出します。![]() 列目の度数の合計を「
列目の度数の合計を「![]() 」、
」、![]() 行目の度数合計を「
行目の度数合計を「![]() 」、すべての度数の合計をnとすると、
」、すべての度数の合計をnとすると、![]() 列・
列・![]() 行目の「理論値」は以下の式から求められます。
行目の「理論値」は以下の式から求められます。
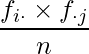
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 男性 | 47.5 | 27 | 20 | 5.5 | 100 |
| 女性 | 47.5 | 27 | 20 | 5.5 | 100 |
| 計 | 95 | 54 | 40 | 11 | 200 |
②「理論値」からの「実測値」のズレを2乗したものを「理論値」で割る
| 血液型 | A型 | O型 | B型 | AB型 | 計 |
|---|---|---|---|---|---|
| 男性 | 100 | ||||
| 女性 | 100 |
③すべての和をとる
和は6.639になります。したがって、![]() =6.639となります。
=6.639となります。
![]() (縦がm行、横がn列)のクロス集計表の場合、自由度が
(縦がm行、横がn列)のクロス集計表の場合、自由度が![]() のカイ二乗分布を用いて検定を行います。この例題の場合(2-1)×(4-1)=3です。したがって自由度「3」の「カイ二乗分布」を使用します。また、独立性の検定は上側P値(右側P値)を参照します。統計数値表から
のカイ二乗分布を用いて検定を行います。この例題の場合(2-1)×(4-1)=3です。したがって自由度「3」の「カイ二乗分布」を使用します。また、独立性の検定は上側P値(右側P値)を参照します。統計数値表から![]() の値を読み取ると「7.815」となっています。
の値を読み取ると「7.815」となっています。
| v | 0.99 | 0.975 | 0.95 | 0.9 | 0.1 | 0.05 | 0.025 | 0.01 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.024 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.345 |
| 4 | 0.297 | 0.484 | 0.711 | 1.064 | 7.779 | 9.488 | 11.143 | 13.277 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.070 | 12.833 | 15.086 |
次の図は自由度3のカイ二乗分布を表したものです。![]() =6.639は図の矢印の部分に該当します。矢印は棄却域に入っていないことから、「有意水準5%において、帰無仮説を棄却しない」という結果になります。つまり「性別と血液型は独立ではないとはいえない(関連があるとはいえない)」と結論づけられます。
=6.639は図の矢印の部分に該当します。矢印は棄却域に入っていないことから、「有意水準5%において、帰無仮説を棄却しない」という結果になります。つまり「性別と血液型は独立ではないとはいえない(関連があるとはいえない)」と結論づけられます。

■イェーツの補正
イェーツの補正は2行×2列のクロス集計表のデータに対して行われる補正で、離散型変数である検定統計量を連続型分布(カイ二乗分布や正規分布)に近似させて統計的検定を行う際に生じる誤差(ズレ)を補正するために用いられます。|(実測値![]() 理論値
理論値![]() |
|![]() )
)![]() を「理論値」で割ることで、イェーツの補正を行ったカイ二乗統計量を算出できます。
を「理論値」で割ることで、イェーツの補正を行ったカイ二乗統計量を算出できます。
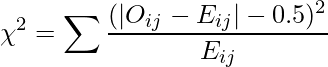
次のようなクロス集計表があるとき、
| 計 | |||
|---|---|---|---|
| a | c | a+c | |
| b | d | b+d | |
| 計 | a+b | c+d | N |
イェーツの補正を行ったカイ二乗値は下式から求められます。ただし、a, b, c, dは各度数を表し、N=a+b+c+dとします。
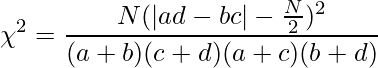
■おすすめ書籍
そろそろ統計ソフトRでも勉強してみようかなという方にはコレ!自分のPC環境で手を動かしながら統計の基礎も勉強しつつRの勉強もできます。結構な厚みがある本です。
25. さまざまな検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 22. 母分散の区間推定
22-1. カイ二乗分布
- 22. 母分散の区間推定
22-2. カイ二乗分布表
- ブログ
独立性の検定
- ブログ
クロス集計表から分析する








