- Step1. 基礎編
- 23. 検定の前に
23-1. 検定とは
統計的仮説検定(単純に「検定」とも言います)は、確率をもとに結論を導く方法です。検定について本格的に学習する前に、まずは検定の基本的な考え方について学びます。
検定は「最初に仮説を立て、実際に起こった結果を確率的に検証し、結論を導く」という手順で行います。結論を導くには「背理法(はいりほう)」を用います。背理法とは「最初に仮説を設定し、仮説が正しいとした条件で考えて矛盾が起こった場合に仮説が間違っていると判断する」方法のことです。具体的な例を用いて検定の流れを見てみます。
例題:
50%の確率で表が出る普通のコインと、10%の確率でしか表が出ない不正なコインがどちらも2枚ずつあるとします。なお、この4枚のコインは全て見た目が同じで見分けることはできません。

「普通のコインだよ」と言われ、普通か不正のどちらかのコイン2枚組を渡されたとします。渡された2枚のコインを投げる試行を2回繰り返したところ、2回ともすべて裏でした。渡された2枚のコインは普通のコインでしょうか、それとも不正なコインでしょうか。
- 仮説を立てる
- 仮説を検定するための「確率」を求める
- 6.25%というのは滅多に起こらない確率だ。つまり渡されたコインは不正なコインに違いない。
- 6.25%というのは低い確率だが、それでも偶然起こることもある確率だ。つまり普通のコインに違いない。
- 判断基準を元に結論を導く
検定を行うにあたっては、まず「仮説」を立てます。ここでは「渡された2枚のコインは普通のコインである」とします。この仮説に矛盾が生じた場合、普通のコインではないと結論付けられます。
渡されたコインが普通のコインであった場合、「2枚とも裏」が2回起こる確率は次のようになります。
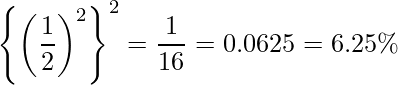
これは、もし普通のコインを渡されていたのであれば6.25%でしか起こらない事象が起こったことを示しています。したがって、6.25%という確率をもとに判断すると、次の2つの結論のどちらかになります。

結論を確定させるために「“滅多に起こらない”と判断する確率の基準」を設定します。例えばこの基準を「10%」と設定すると、10%以下の確率で起こる事象については「滅多にないこと」であるため、「仮説が間違っている」と判断されます。逆に、10%以上の確率で起こる事象については、「滅多にないことではない=許容できる範囲」となるため、「仮説が間違っているとは言えない」と判断されます。
この問題では、仮説を「渡されたコインは普通のコインである」とし、観測した事象が起こる確率は6.25%でした。6.25%は判断基準10%より小さいため「渡されたコインは普通のコインであるとは考えられない」という結論を導くことができます。

【コラム】検定を行う上での注意点
■導かれた結論は「絶対に正しい」と考えることはできない
「滅多にないことである」と結論付けられたとしても、6.25%という確率は「仮説が正しくても、16回に1回は起こってもおかしくない」出来事であるとも考えられます。検定は確率をもとに判断を行うので、結論が絶対に正しいと考えることはできません。
■「滅多にない」とする基準は先に決めておかなくてはならない
6.25%という確率を知った後で「滅多にない」基準を設定すると、例えば次のような恣意的(しいてき)な誘導ができます。すなわち、後出しじゃんけんのように自由に結論を変えることができてしまいます。そのため、「滅多にない」基準は、実験や試行を行う前に決めておかなくてはなりません。
- 6.25%は滅多に起こらないことだと考えられる。だから、基準を「10%」にして、不正なコインと結論付けよう。
- 不正なコインだと断言するのは避けたいから、基準を5%にしておこう。(もしも「滅多にない」基準を5%とすると、6.25%>5%であるため、「普通のコインであると考えられる」という全く逆の結論になってしまいます)
■おすすめ書籍
このあたりで一度、ここまで学んできた範囲の統計学の実力をチェックしてみてはいかがでしょうか。手元に電卓(×関数電卓)を準備してぜひ!








