- Step1. 基礎編
- 30. 二元配置分散分析
30-4. 二元配置分散分析の分散分析表4
30-1、30-2、30-3章では交互作用を含む分散分析表の作成を行いました。30-1章で示したデータは1つの水準(例えば肥料100g・土A)に3つのデータが含まれています。このようなデータの場合には「繰り返しのある二元配置分散分析」を行い、交互作用を算出することができます。
一方、次の表のように、1つの水準に含まれるデータが1つである場合には「繰り返しのない二元配置分散分析」を行います。繰り返しのない二元配置分散分析では交互作用を算出することができません(交互作用を残差変動から分離できません)。
次の表はある作物の収量(kg)についてまとめたものです。肥料の量4パターンと、土をAとBの2種類を用いて、計8通りの生育環境において各1回の実験を行いました。このデータから、各因子(肥料の量、および土の種類)の水準間で収量の平均値に差があるかどうかを二元配置分散分析で検定します。帰無仮説![]() は「各因子の水準間で作物の収量の平均値は等しい」とします。
は「各因子の水準間で作物の収量の平均値は等しい」とします。
| 肥料 100g | 肥料 200g | 肥料 300g | 肥料 400g | |
|---|---|---|---|---|
| 土A | 14.5 | 16.5 | 17.8 | 18.1 |
| 土B | 16.2 | 18.6 | 21.7 | 23.6 |
■平均値について
分散分析表を埋めるために、さまざまな平均値を求めます。
- 【全体】すべてのデータの平均値:18.38
- 【肥料の量ごとの平均値】肥料100g:15.35、肥料200g:17.55、肥料300g:19.75、肥料400g:20.85
- 【土の種類ごとの平均値】土A:16.73、土B:20.03
■平方和について
- 全体の平方和
- 肥料の量の平方和
- 土の種類の平方和
「全体の平方和」は「データ全体の平均値からの各データのズレ」を求めたものです。
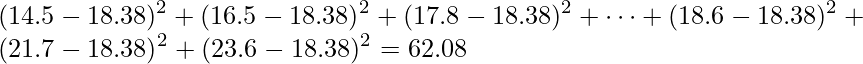
「肥料の量の平方和」は「データ全体の平均値からの肥料の量の各水準の平均値のズレ」を求めたものです。
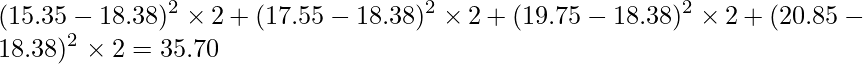
「土の種類の平方和」は「全体の平均値からの土の種類の各水準の平均値のズレ」を求めたものです。
■自由度について
- 全体の自由度
- 肥料の量の自由度
- 土の種類の自由度
「全体の自由度」は全てのデータの個数から1を引いたものになります。したがって「8-1=7」になります。
「肥料の量の自由度」は肥料の量の水準数から1を引いたものになります。したがって「4-1=3」になります。
「土の種類の自由度」は土の種類の水準数から1を引いたものになります。したがって「2-1=1」になります。
■残差について
「残差の平方和」は「全体の平方和」から「肥料の量の平方和」、「土の種類の平方和」を引いたものになります。
「残差の自由度」は「全体の自由度」から「肥料の量の自由度」、「土の種類の自由度」を引いたものになります。したがって「7-3-1=3」になります。
■平均平方について
最後に「平均平方」を求めます。平均平方は「平方和」を「自由度」で割ったもので、「全体」以外の因子について求めます。
肥料の量:35.70/3=11.90
土の種類:21.78/1=21.78
残差:4.60/3=1.53
■F値について
統計量Fは「各因子の平均平方」を「残差の平均平方」で割って算出します。
肥料の量:11.90/1.53=7.78
土の種類:21.78/1.53=14.24
■分散分析におけるF検定について
ここまでの結果を分散分析表にまとめると次のようになります。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 肥料の量 | 35.70 | 3 | 11.90 | 7.78 |
| 土の種類 | 21.78 | 1 | 21.78 | 14.24 |
| 残差 | 4.60 | 3 | 1.53 | |
| 全体 | 62.08 | 7 |
- 肥料の量
- 土の種類の自由度
自由度(3,3)のF値(9.28)を用いて検定を行います。分散分析から得られた統計量Fは7.78であることから、有意水準5%ではF分布表から読み取ったF値と比較して小さくなっています。したがって、「肥料の量によって収量の平均値に差がある」とは言えません。
自由度(1,3)のF値(10.13)を用いて検定を行います。分散分析から得られた統計量Fは14.24であることから、有意水準5%ではF分布表から読み取ったF値と比較して大きくなっています。したがって、「土の種類によって収量の平均値に差がある」と結論付けられます。
■各水準の母平均の信頼区間
繰り返しのない二元配置分散分析において、因子Aにおける水準![]() 、Bにおける水準
、Bにおける水準![]() の母平均の信頼区間はそれぞれ次の式から求められます。
の母平均の信頼区間はそれぞれ次の式から求められます。
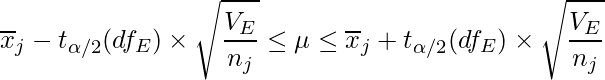
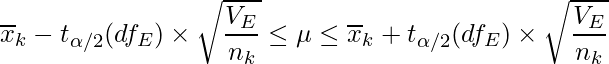
![]() と
と![]() は各水準
は各水準![]() と
と![]() の標本平均を、
の標本平均を、![]() は残差の自由度を、
は残差の自由度を、![]() は残差の平均平方を、
は残差の平均平方を、![]() と
と![]() は水準
は水準![]() と
と![]() におけるサンプルサイズを表します。
におけるサンプルサイズを表します。







