カプラン=マイヤー法 : Kaplan-Meier Method
概要
カプラン=マイヤー法により生存関数を推定し、生存率曲線を作成します。5群まで実行可能で、2群以上の場合、ログランク検定(Log rank Test)と一般化Wilcoxon検定(Generalized Wilcoxon Test)により生存率曲線の差の検定の結果も出力します。
本製品では、「状態情報」はイベント発生を1、打ち切りを0として分析します。
表形式とは、「イベント発生時間情報」1列と「状態(打ち切り・死亡等)情報」1列の計2列が群ごとに分けられているデータを指します。この場合、メニューから「カプラン=マイヤー法(表形式)」を選択して分析を開始してください。 データベース形式とは、「群情報」、「イベント発生時間情報」、「状態(打ち切り・死亡等)情報」がそれぞれ1列にまとめられているデータを指します。この場合、メニューから「カプラン=マイヤー法(データベース形式)」を選択して分析を開始してください。
生存率曲線の差の検定
本製品では、ログランク検定と一般化Wilcoxon検定を搭載しています。一般化Wilcoxon検定が相対的に初期に起きた死亡を重く評価するのに対し、ログランク検定は後期の死亡を重く評価します。すなわち、時間経過と共に生存率曲線の差が開いてくるような場合、ログランク検定は一般化Wilcoxon検定に比べて検出力が高くなります。また、生存率曲線が交差するような場合、いずれの手法も検出力が低くなります。
- ログランク検定
- 本製品では、Peto-Peto(ピトー=ピトー)による方法とCochran-Mantel-Haenszel(コクラン=マンテル=ヘンツェル)による方法の2種類のログランク検定を行います。Peto-Petoによる方法は計算方法が簡便ですが、Cochran-Mantel-Haenszelによる方法に比べて少し保守的で有意になりにくい性質があります。単にログランク検定という場合、一般にCochran-Mantel-Haenszelによる方法のことを指します。
- 一般化Wilcoxon検定
- 本製品では、Gehan-Breslow(ゲーハン=ブレスロウ)による方法とPeto-Prentice(ピトー=プレンティス)による方法の2種類の一般化Wilcoxon検定を行います。Gehan-Breslowによる方法は、初期に非常に多くの打ち切りがある場合、最初の数例の死亡でほとんど結果が決まってしまいます。また、打ち切りのパターンに依存して大きく結果が異なる欠点もあります。これらの欠点を改善したものがPeto-Prenticeによる方法となります。打ち切りがない場合、Gehan-Breslowによる方法とPeto-Prenticeによる方法の結果は等しくなります。
※ 詳細につきましては、大橋・浜田(1995) をご参照ください。
分析例ファイルのダウンロード
カプラン=マイヤー法を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
カプラン=マイヤー法(表形式)の場合
| データサイズ範囲 | 処理対象データ | |||
|---|---|---|---|---|
| 行数 | 列数 | 数値 | 文字列 | 空白 |
| 3~10,000行 | 2~10列(5群までのデータ) | ○ | 欠 | 欠 |
※:○…処理可、×…処理不可、欠…欠損値として除く
表形式の具体例と仕様
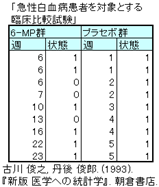
- 3行以上のデータがあること
- 1つのデータ(各行)には、イベント(打ち切り・死亡等)の発生した「時間」情報と「状態」情報が含まれていること。また、「時間」と「状態」の情報はそれぞれ1列にまとめられていること。
- 「状態」情報は0/1のデータであること。ただし、0を打ち切り、1をイベント発生とする。
カプラン=マイヤー法(データベース形式)の場合
| データサイズ範囲 | 処理対象データ | |||||
|---|---|---|---|---|---|---|
| 行数 | 列数 | 判別群 | 数値 | 文字列 | 空白 | |
| 時間 | 3~60,000行 | 1列 | - | ○ | 欠 | 欠 |
| 状態 | 3~60,000行 | 1列 | - | ○ | 欠 | 欠 |
| グループ変数 | 3~60,000行 | 1列 | 2~5群 | ○ | ○ | 欠 |
※:○…処理可、×…処理不可、欠…欠損値として除く
データベース形式の具体例と仕様

- 3行以上のデータがあること
- 「グループ変数」、「時間」、「状態」がそれぞれ1列ずつにまとめられていること
- 時間列と情報列以外に群情報の列があること
- 「状態」情報は0/1のデータであること。ただし、0を打ち切り、1をイベント発生とする
設定項目
Excelの[エクセル統計]タブから、[生存分析・ハザード分析]→[カプラン=マイヤー法(表形式)]もしくは[カプラン=マイヤー法(データベース形式)]を選択すると以下のダイアログが表示されます。
カプラン=マイヤー法(表形式) ダイアログ

- データ入力範囲 必須
- 各群2列ずつ5群までの範囲を指定できます。各群のデータを左から「時間」「状態」の順で構成し、状態データは「0」を打ち切り、「1」をイベント発生としてください。「空白」や「文字」のセルを含むケースを除いて計算を行います。
- ラベル 必須
- データ入力範囲に含まれるラベルとして、[先頭 2行をラベルとして使用する] (初期設定)、[先頭行を時間と状態のラベルとして使用する]、[ラベルなし]のいずれかを選択します。
- 曲線上の打ち切り例をマークで表示する
- 生存率曲線上の打ち切り例にマークをつける場合、このチェックボックスをオンにします。初期設定はオフになっています。
- 曲線を1-生存率で描く
- 1-生存率の曲線を描く場合、このチェックボックスをオンにします。初期設定ではオフになっています。
- 累積生存率の95%信頼区間の算出方法 必須
- [変換無し]、[対数変換]、[二重対数変換]、[逆正弦変換]、[ロジット変換]の5種類の手法から1つを選択します。初期設定は [変換無し] になっています。
カプラン=マイヤー法(データベース形式)ダイアログ 「変数」タブ
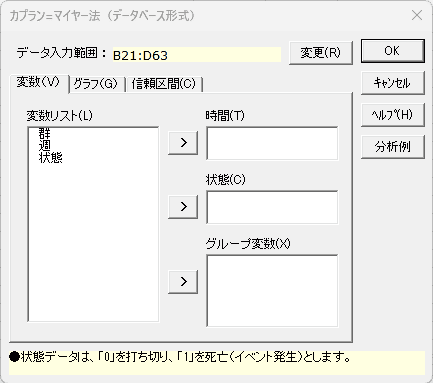
- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力範囲のダイアログが表示されるので、データ入力範囲を設定して [変更] ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- 時間 必須
- [変数リスト]から時間データを選択します。
- 状態 必須
- [変数リスト] から状態データを選択します。
- グループ変数 必須
- [変数リスト]からグループ変数を選択します。グループ変数として選択できるのは1変数のみです。
カプラン=マイヤー法(データベース形式)ダイアログ 「グラフ」タブ
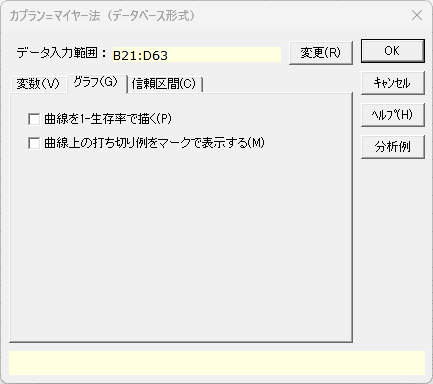
- 曲線を1-生存率で描く
- 1-生存率で曲線を描く場合、このチェックボックスをオンにします。初期設定ではオフになっています。
- 曲線上の打ち切り例をマークで表示する
- 生存率曲線上の打ち切り例にマークをつける場合、このチェックボックスをオンにします。初期設定はオフになっています。
カプラン=マイヤー法(データベース形式)ダイアログ 「信頼区間」タブ
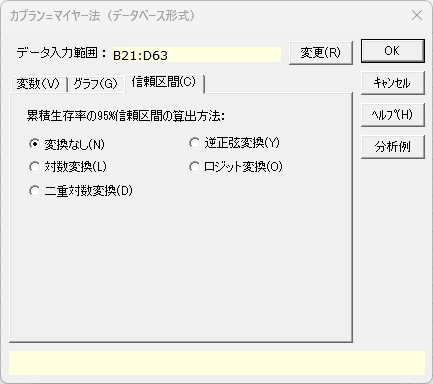
- 累積生存率の95%信頼区間の算出方法 必須
- [変換無し]、[対数変換]、[二重対数変換]、[逆正弦変換]、[ロジット変換]の5種類の手法から1つを選択します。初期設定は [変換無し]になっています。
出力内容
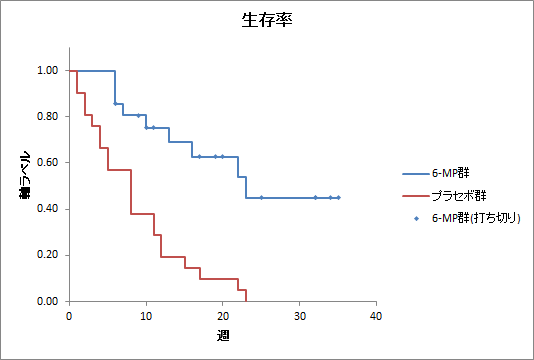
| 【グラフ】生存率 | カプラン=マイヤー法による生存率曲線のグラフが出力されます。[曲線を1-生存率で描く]にチェックを入れた場合、1-生存率のグラフになります。 |
|---|---|
| ケースの要約 | 各群の「死亡」、「打ち切り」、「全体」の件数 |
| 生存時間の平均値と中央値 | 各群の生存時間の「平均値」と「中央値」、それぞれに対する「標準誤差」と「95%信頼区間」が出力されます。平均値は打ち切りを含む全観察期間における生存時間の平均値を、中央値は半分の被験者が亡くなった時点までの時間を示します。 |
| 生存率曲線の差の検定 | ログランク検定(Peto-Peto、Cochran-Mantel-Haenszel)、一般化Wilcoxon検定(Gehan-Breslow、Peto-Prentice)の4手法を用いて、帰無仮説:「すべての群の生存関数は等しい」についてカイ二乗検定を行った結果です。データが2群以上の場合に出力されます。 |
| 生存率表 | 各群における時間経過に伴う「死亡」、「打ち切り」、「残数」、「累積生存率(または累積死亡率)」、「標準誤差」、累積生存率の「95%信頼区間」が出力されます。「95%信頼区間」の「上限値」と「下限値」は信頼区間算出方法で選択した計算方法により算出されます。 |
| グラフ用データ | 生存率曲線作成用のデータ |
スライドによる使い方の説明
エクセル統計の使い方(カプラン=マイヤー法編) from Social Survey Research Information Co., Ltd.
参考文献
- 赤澤 宏平, 柳川 尭, "サバイバルデータの解析―生存時間とイベントヒストリデータ (バイオ統計シリーズ)", 近代科学社, 2010.
- 大橋 靖雄, 浜田 知久馬, "生存時間解析―SASによる生物統計", 東京大学出版会, 1995.
- 高橋 信, "すぐ読める生存時間解析―カプラン=マイヤー法/ロジスティック回帰分析/コックスの比例ハザードモデルが、よくわかる!", 東京図書, 2007.
- 丹後 俊郎, 古川 俊之, "医学への統計学", 朝倉書店, 2013.>
- 臨床評価研究会(ACE)基礎解析分科会, "実用SAS生物統計ハンドブック―SAS 8.2及びSAS 9.1対応", サイエンティスト社, 2005.


